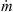| Issue |
Dairy Sci. Technol.
Volume 90, Number 2-3, March–June 2010
Special Issue: Selected papers from 4th International Symposium on Spray Dried Dairy Products, 15-17th April 2009, Melbourne, Australia |
|
|---|---|---|
| Page(s) | 181 - 210 | |
| DOI | https://doi.org/10.1051/dst/2009059 | |
| Published online | 09 February 2010 | |
Review
One-dimensional simulation of co-current, dairy spray drying systems – pros and cons
乳粉顺流喷雾干燥系统一维模拟的利弊分析
Simulation monodimensionnelle de systèmes de séchage par atomisation de produits laitiers en co-courant – avantages et inconvénients
1
Biotechnology and Food Engineering Group, Department of Chemical Engineering, Monash University, Clayton Campus, Victoria 3800, Australia
2
INRA, UMR1253, F-35042 Rennes, France
3
AGROCAMPUS OUEST, UMR1253, F-35042 Rennes, France
* Corresponding author (通讯作者): dong.chen@eng.monash.edu.au
Received:
15
June
2009
Revised:
12
November
2009
Accepted:
18
December
2009
One-dimensional (1-D) simulation is a useful technique for the evaluation of dryer operating parameters and product properties before conducting real spray drying trials. The main advantage of a 1-D simulation tool is its ability to perform fast calculations with significant simplicity. Mathematical models can be formulated using heat, mass and momentum balances at the droplet level to estimate time-dependent gas and droplet parameters. One of the purposes of this paper is to summarize key mathematical models that may be used to perform 1-D simulation for spray drying processes, predict essential product-drying gas parameters, assess the accuracy of prediction using pilot-scale spray drying data and perhaps most importantly address the main benefits and limitations of the 1-D simulation technique in relation to industrial spray drying operations. The results of a recent international collaborative study on the development of spray drying process optimization software for skim milk manufacture are presented as an example of the application of 1-D simulation in milk processing.
摘要
一维模拟是在进行实际喷雾干燥之前用来评价干燥器操作参数和产品特性的一种技术方法。 一维模拟最大的优点是可以用简单的方法进行快速计算。 根据液滴的热、质量和动力平衡的数学方程来估算时间-气体的关系以及液滴的参数。本文概述了一些重要的、实用的一维模拟的数学模型,这些模型可以用来预测喷雾干燥过程,预测产品干燥的气体参数,评定中试级喷雾干燥预测数据的准确性;以及着重分析了一维模拟技术在喷雾干燥工业生产中的利与弊。最近国际上合作开发出的用于脱脂乳喷雾干燥生产工艺参数优化的软件就是一维模拟技术在乳品加工中最好的应用实例。
Résumé
La simulation monodimensionnelle (1-D) est une technique utile pour évaluer les paramètres de séchage et les propriétés des produits avant de conduire les essais de séchage en réel. Le principal avantage de l’outil de simulation 1-D est sa capacité à réaliser des calculs rapidement et avec une grande simplicité. Les modèles mathématiques peuvent être formulés avec les équilibres de chaleur, de masse et de quantité de mouvement à l’échelle de la gouttelette pour estimer les paramètres de vapeur et de gouttelette qui varient au cours du temps. Un des objectifs de cet article est de présenter de façon synthétique les modèles mathématiques clés qui peuvent être utilisés pour réaliser une simulation 1-D, prédire les paramètres de vapeur essentiels pour le séchage du produit, évaluer la précision de la prédiction en utilisant les données du séchage par atomisation obtenues à l’échelle pilote, et enfin d’aborder les principaux bénéfices et limites de la technique de simulation 1-D en relation avec les opérations de séchage par atomisation industrielles. Les résultats d’une récente étude réalisée en collaboration internationale sur le développement d’un logiciel d’optimisation du procédé de séchage par atomisation pour la production de poudre de lait écrémé sont présentés pour illustrer l’application de la simulation 1-D.
Key words: spray drying / one-dimensional simulation / modeling / drying kinetics / dairy product / droplet drying
关键字 : 喷雾干燥 / 一维模拟 / 模型 / 干燥动力学 / 乳制品 / 液滴干燥
Mots clés : séchage par atomisation / simulation mono-dimensionnelle / modélisation / cinétique de séchage / produit laitier / séchage d’une gouttelette
© INRA, EDP Sciences, 2010
1. INTRODUCTION
In the current environment of economical crisis and strict climate policies, industries in almost all sectors are striving to improve process efficiencies or to adopt new technologies so that energy and water consumption, manufacturing cost and carbon emission can be minimized. This is particularly evident in the dairy and food processing industries. Replacing or modifying conventional techniques by newer cost effective technologies may not be straightforward because one has to carefully study the requirement of additional capital costs, the availability of resources and personnel, the influence on product quality and the risk of “using it first time”. It is a challenge to all dairy manufacturing researchers to develop innovative approaches for reducing processing costs and energy consumption during drying operations while maintaining top product quality in such a way that a minimum additional investment (time, money and resources) is needed.
Spray drying is a relatively high energy-intensive operation because the water (or solvent) is removed mainly using thermal energy. The energy needed to remove a kilogram of water during single or multi-stage spray drying is usually 10–20 times higher than the energy required during multi-pass evaporation to remove the same amount of water [9, 80]. Furthermore, all large-scale spray drying industries currently rely on fossil fuels to provide the energy needed for water removal. Keeping the strict climate policies in mind, there is a need to recover the energy from exhaust streams and look for alternative “green” energy resources.
Apart from energy reduction and/or recovery during spray drying operations, product quality improvement, new product development and minimizing other potential problems such as wall deposition and stickiness are major concerns for dairy powder manufacturers. To understand how chemical and process engineers can address these issues, it is important to understand the relationship between product quality, process parameters and equipment design. When the physical principles of modeling are defined, simulation can be a useful technique to mathematically characterize various drying phenomena occurring during spray drying and establish relationships between key process and quality parameters. Reviewing the current set of drying/feed parameters and tuning these parameters based on a more reliable optimization technique may be helpful in dealing with several critical issues without the need for new equipments or major changes to process design.
Simulation is essentially an approximation technique or tool that can provide predictions and trends of process and product parameters with acceptable accuracies. Simulation techniques are increasingly becoming popular in the software development community to optimize spray drying processes and predict product properties before conducting real spray drying trials. As a precaution it should be noted that simulation is not a unique “remedy” to all operational problems. The predictive power and the reliability of simulation techniques largely depend on the appropriateness of the mathematical models used and how well they are validated. A programmer should be aware of the extent of details required from simulation tools because this information is directly linked with the complexity of simulation programs and the time, resources and skills required. Different scales of mathematical analysis and a variety of process calculation tools can be employed depending on the type of information required from a simulation.
Simulation may be helpful to process engineers in following ways:
-
Traditionally, optimization and generation of new process parameters and drying kinetic data were realized using experimental trials that were expensive and eventually risky. Simulation can greatly reduce the experimental trials required to study various drying phenomena and the associated trends upon changing process parameters. Drying processes can be pretested in this way using a set of appropriate mathematical models. Simulation thus helps in minimizing product testing time, resources, hazards, energy consumption and wastage. This can be considered a significant advantage.
-
Simulation can also provide early insights for equipment design and new processes development as well as for scale-up, scale-down, process and quality control and risk management during spray drying.
-
Simulation permits the development of a process-product integrated approach that helps in studying process and product parameters together. Thus, it can be helpful in estimating energy consumption, process efficiencies, production costs and product quality sensitivity to the changes in process and feed parameters.
-
Simulation can be of a great benefit for training and education purposes at production sites, academic institutes and R&D centers.
2. SIMULATION OF SPRAY DRYING
A significant extent of research has been conducted to mathematically characterize various phenomena occurring during spray drying. Unfortunately a unique theoretical approach to characterize drying phenomena (e.g. drying kinetics, particle trajectories, and gas-flow pattern) and to design associated equipments does not exist [59]. One of the reasons for this is the complexity of the spray drying process, which includes many aspects of transport phenomena, fluid mechanics, heat and mass transfer, reaction engineering, particle engineering as well as material science [15]. Mathematical analysis and simulation can become very complex when all these drying principles are considered together. Based on the complexity of mathematical analysis, simulation approaches may be classified as follows.
2.1. “Zero”-dimensional (course-scale) simulation approach
In this approach, the spray dryer is essentially considered as a “black box”. Drying processes are simulated using overall heat and mass balance equations to predict gas temperature, gas humidity and product moisture content at the inlet or outlet of dryers [10]. Drying chambers are mostly treated as well-mixed reactors [30, 95, 110]. Calculations for heat and mass balances over spay dryers and fluidized-bed dryers are usually done separately. The drying kinetics model is mostly not incorporated for this course-scale simulation approach. This approach can provide “first-draft” information regarding gas and product conditions at the inlet and outlet of the drying chambers by simply using a scientific calculator or an Excel spreadsheet. Recently, Langrish [47] illustrated how this course-scale approach can be used to estimate a product’s sticky-point temperature at the outlet of the spray dryer in order to predict stickiness behavior of the powder.
2.2. “1-D” (finer-scale) simulation approach
In the 1-D simulation approach, mass, heat and momentum balances are performed at an individual droplet level by following drying time or dryer height [72, 73]. Drying kinetics is incorporated in this approach which allows predicting drying-rate profiles and identifying fast and slow drying-rate periods. It is usually considered that hot gas and droplets are moving in parallel within the drying chambers [70]. This simulation approach is widely used to model product characteristics during spray drying where tall-form spray dryers were used [72, 109, 110, 112]. A major advantage of the 1-D approach is the capability to evaluate the “average” behavior (temperature, moisture concentration and velocity profiles) of the powder and hot gas following drying time or dryer height integration. These profiles can assist in predicting various thermo-physical properties and quality parameters of the product throughout drying [73]. A relatively simple Excel spreadsheet is usually sufficient to build effective 1-D spray drying simulation software.
2.3. “2-D” and “3-D” (finest-scale) simulation approaches
Zero-D and 1-D simulation approaches cannot effectively reveal information on gas-flow patterns, time-dependent particle trajectories, atomizer performance, agglomeration, wall deposition and gas-particles residence time data. Such information is crucial for scale-up, scale-down and equipment design, and can be obtained using 2-D and 3-D simulation approaches. In these multi-scale simulation approaches, the basic processes happening in the dryer are discretely classified with respect to space and time to apply the associated physical and chemical principles on individual droplets. Drying-rate profiles of these droplets can be predicted using appropriate drying kinetics models. Simple and effective lumped-parameter models (which do not provide internal temperature-moisture profiles within the droplets) are usually desired for 2-D and 3-D simulations due to their simplicity and speed during computation. Several publications have comprehensively reported how 2-D and 3-D simulation approaches using various CFD packages (e.g. Fluent and CFX) can be helpful to predict agglomeration behavior during spray drying [33, 49, 97], evaluate particle trajectories [11], design new drying chamber configurations and assess atomizer performance [11, 36–38] as well as to study gas distribution within drying chambers [11, 28, 33, 34, 45, 50, 53, 68, 93, 101, 111]. The accuracy of prediction by finer-scale approaches mainly depends on the selection of mass-heat-momentum conservation equations, the accuracy of turbulence models, the appropriateness of numerical methods used for solving equations and the quality of grid generation and algorithm development [28, 47, 50]. Recently, Langrish [47] outlined important advantages and current challenges of 2-D and 3-D simulation approaches. In spite of their ability to provide fine details of drying processes, the use of 2-D and 3-D simulation approaches is not common in industrial control rooms (especially dairy and food processing industries) due to the high cost of computational package licenses, long simulation time (usually a few hours to several weeks or even months for large-scale spray dryers) and the requirement for programming experience and skilled personnel. CFD simulation of spray drying processes is now becoming more popular and industrially feasible due to the availability of fast computation machines and new powerful CFD packages [38].
In this paper, the main focus is on how the 1-D simulation approach can be helpful in optimizing industrial spray drying operations, the components that may be required to build an effective simulation tool and the important pros and cons of this 1-D approach.
3. ONE-DIMENSIONAL SIMULATION
The 1-D simulation approach has previously been used to model spray drying operations due to its ability to predict a product’s moisture, temperature and velocity profiles throughout drying [30, 31, 48, 66, 70, 72, 73, 109, 112]. Three main components to formulate the 1-D simulation tool for modeling spray drying processes are (1) drying kinetics data from laboratory-scale experiments and drying kinetics model, (2) a set of appropriate mathematical equations, and (3) a process calculation tool (e.g. Excel and MATLAB).
3.1. Drying kinetics
Drying kinetics is a key element in predicting a material’s drying behavior and product quality. Drying kinetics models allow for predicting fast and slow drying periods in the drying chamber. Due to increased resistances to heat-mass transfer during drying, the drying rate significantly slows down during the later drying period and will affect the overall drying time. Measurement of drying kinetics from laboratory-scale experiments and fitting of measured data with an appropriate drying kinetics model are important steps to perform mathematical modeling and simulation. The appropriateness of a drying kinetics model and the accuracy of laboratory drying kinetics data will have a direct influence on the accuracy of prediction by 1-D simulation tools.
3.1.1. Drying kinetics measurement
A simple approach for predicting the quality of dried powders is to understand (and accurately model) what a single droplet/particle actually experiences during its flight in the drying chambers regarding its temperature and moisture content, and how a single droplet/particle may respond to these changes [18]. Several laboratory-based techniques have been described in the literature to measure drying kinetics data for use in developing a drying kinetics model for spray drying. Four commonly used techniques are:
-
Suspended droplet drying: Suspended droplet drying is the most common technique used to obtain drying kinetics data [2, 3, 17, 27, 55, 99]. This technique is also used to study volatile retention [62] and morphology changes [5] during spray drying. In this method, small (1–3 mm), single droplets are suspended in a small drying chamber using a thin glass filament or similar means. Droplets are dried using hot air of constant temperature, velocity and humidity. Changes in the droplet’s weight, temperature and diameter are recorded through independent experiments in order to determine a characteristic behavior of materials under drying conditions. This technique is popular due to its simplicity and also because both spray drying processes and suspended droplet drying techniques deal with spherical droplets.
-
Thin-layer drying: In this technique, materials are dried in a thin-layer (or slab) form in order to record changes in the sample’s temperature, weight and thickness [6, 19, 20, 24, 58]. The effective area for heat-mass transfer is assumed to be constant when estimating drying flux. Experimental data are used to determine drying kinetics parameters or characteristic behavior of materials which can be used to model spray drying processes.
-
Droplet drying using acoustic levitation: In this method, single droplets are suspended using strong acoustic fields in an acoustic levitator. Changes in the droplet’s temperature and diameter are measured using infrared thermal devices and digital camera/recorders, respectively [32, 42, 51, 85, 86, 92, 103, 105–108]. Moisture content profiles are estimated either from diameter profiles or often using a hygrometer to measure the outlet air humidity from the closed levitator. The role of internal water circulation within acoustically suspended droplets and the effects of acoustic fields on internal water diffusion and total evaporation have not yet been clearly described. Recently, GEA Niro developed a simulation tool (DRYNETICS™) by combining droplet drying data obtained from acoustic levitation experiments and a CFD package in order to assist in optimizing spray dryer performance.
-
Desorption method: Drying by desorption is another simple method to measure water availability or drying behavior of materials [87, 88]. Liquid material is dried in the form of a thin disk using a small plastic cup that is placed in a closed container filled with zeolite (or other adsorbents) particles. This container is placed in the oven where liquid concentrates are dried at around 45 °C that is believed to be an approximate wet-bulb temperature for water evaporation in real spray dryers [87]. The relative humidity profile in the container is continuously recorded using a sensor that is usually placed very close to the surface of liquid samples in the container. From the relative humidity profiles, moisture content profiles of the liquid samples can be evaluated. Recently, Schuck et al. [87] developed and licensed a spray drying simulation software (SD2P®) by combining the relative humidity profiles obtained by the desorption method and the overall heat-mass balances (using a “black box” approach) in order to optimize drying conditions for large-scale spray dryers.
3.1.2. Drying kinetics approaches
Once drying kinetics data are measured from laboratory-based experiments, these measured data are correlated with an appropriate drying kinetics approach to formulate a model and predict a time-dependent “average” drying flux. The appropriateness and accuracy of the drying kinetics model will affect the accuracy of prediction for a product’s behavior, quality parameters and stickiness data [17, 73, 76]. In the literature, several drying kinetics approaches have been proposed for the modeling of spray drying processes. Each approach is formulated based on various simplifications and has its own advantages and drawbacks. The ease of usage, appropriateness and accuracy should be considered for selecting a right approach for particular applications. Four main types of drying kinetics approaches have been commonly used in the literature:
-
Reaction engineering approach (REA)
-
Characteristic drying curves (CDC) approach
-
Internal moisture diffusion-based approaches
-
Receding interface (or moving boundary) approaches.
The CDC and REA are lumped-parameter approaches and predict “average” behavior of products under drying conditions. The CDC and REA have been widely used in the literature to model droplet drying processes as well as large-scale spray drying processes, because both these approaches are fairly simple to use and hold physical meanings of the drying process. The REA has been reported to be more accurate by various studies [17, 73]. Patel and Chen [73] effectively used the REA and CDC approaches to predict and compare product quality parameters during spray drying using a spreadsheet-based 1-D simulation tool. The REA and CDC approaches have also been successfully incorporated into CFD simulations to study spray drying phenomena [35, 41, 100, 102]. Recently, Jin and Chen [41] used the REA in CFD modeling to simulate an industrial-scale spray dryer for studying gas-flow patterns, particle trajectories, gas-particles residence time data and temperature and moisture content profiles of powders. They found the REA to be effective and simple to use because it does not require the modeling for constant and falling drying-rate periods separately unlike the CDC approach.
Diffusion-based [2, 1, 25–27, 44, 60, 61, 83] and receding interface-based [22, 23, 46, 63, 64, 84] drying kinetics approaches deal with spatial moisture and/or temperature distribution within droplets, and may be useful to predict surface morphology. The latter drying kinetics approaches require solving a set of partial differential equations using appropriate numerical methods; therefore, further complexity is involved when these models are incorporated into simulation tools. Moreover, a careful measurement of moisture diffusivity from laboratory-scale experiments is required to use these diffusion-based and receding interface-based drying kinetics approaches [16, 52, 81, 113]. Evaluating and modeling the moisture diffusivity through laboratory-scale experiments is difficult and time-consuming [4, 14, 52, 81].
An example is provided in this study to show how the REA model can be used in conjunction with laboratory-scale and pilot-scale experimental data to develop a 1-D simulation tool for predicting the drying behavior of skim milk.
3.1.3. REA
The REA is a relatively new approach, first introduced by Chen and Xie [20] and modified by Chen and Lin [17] based on careful experimentation on the drying of milk droplets. The REA has successfully been used to conduct dryer-wide simulations for large-scale spray dryers [73–75]. In these studies, the REA appeared to be simple, effective and sensitive to the majority of the drying parameters. In the original model proposed by Chen and Lin [17], the effect of initial moisture content was not taken into account while evaluating the liquid concentrate’s relative activation energy, an important parameter of the REA. In other words, a single “fingerprint” was used to model liquid concentrates of all initial moisture concentrations. This led to the overestimation of the relative activation energy profiles (or underestimation of drying flux profiles) for liquid materials of low initial moisture concentrations. Recently, Patel et al. [79] modified the approach by considering the effect of initial moisture contents which provided an individual relative activation energy profile for liquid concentrates of each initial moisture content. This modified REA model was found more accurate when simulating the drying of sugar droplets in the work of Patel et al. [79].
In the case study provided in this paper, the modified REA was incorporated into the 1-D simulation tool to deliver the predictions of important feed/gas profiles. When using the REA, the rate of water evaporation or drying flux can be estimated using the following equation [17, 79]:![$$ -\frac{\mathrm{d}{m}_{\mathrm{w}}}{\mathrm{d}t}=-{m}_{\mathrm{s}}\frac{\mathrm{d}\bar{X}}{\mathrm{d}t}={h}_{\mathrm{m}}{A}_{\mathrm{p}}\left[{\rho }_{\mathrm{v},\mathrm{sat}}\enspace \mathrm{exp}\left(-\frac{\Delta {E}_{\mathrm{v}}}{{R}_{\mathrm{g}}{T}_{\mathrm{p}}}\right)-{\rho }_{\mathrm{v},\mathrm{b}}\right], $$](/articles/dst/full_html/2010/02/dst0979/dst0979-eq1.gif) (1)where m
w (kg) and m
s (kg) are the weights of water and solids in the droplet,
(1)where m
w (kg) and m
s (kg) are the weights of water and solids in the droplet, 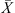 (kg·kg−1, dry basis) is the droplet’s average moisture content, ρ
v,sat (kg·m−3) is the saturated vapor concentration corresponding to average droplet temperature (T
p), ρ
v,b (kg·m−3) is the vapor concentration of bulk drying gas, h
m (m·s−1) is the average mass-transfer coefficient, A
p (m2) is the droplet’s surface area and ΔE
v (J·kg−1) is the apparent activation energy.
(kg·kg−1, dry basis) is the droplet’s average moisture content, ρ
v,sat (kg·m−3) is the saturated vapor concentration corresponding to average droplet temperature (T
p), ρ
v,b (kg·m−3) is the vapor concentration of bulk drying gas, h
m (m·s−1) is the average mass-transfer coefficient, A
p (m2) is the droplet’s surface area and ΔE
v (J·kg−1) is the apparent activation energy.
The first term on the right-hand side of equation (1) (ρ v,sat terms) is the zero-order drying “reaction” that is the activation process. The second term on the right (ρ v,b terms) is the first-order wetting “reaction”. Thus, the rate of moisture removal was seen as a competitive process between drying and wetting reactions. The apparent activation energy parameter (ΔE v) was normalized using an “equilibrium” or “maximum” activation energy (ΔE v,b) to define a new dimensionless parameter called “relative activation energy” (ΔE v/ΔE v,b) [71, 79].
An exponential term in equation (1) is water activity at the droplet’s surface and it was correlated with the droplet’s average moisture content [17, 20]. A similar drying kinetics approach was adopted by Bernard et al. [7] who correlated the surface water activity with the droplet’s average moisture content using an Oswin-type empirical equation unlike the REA’s relative activation energy function. The relative activation energy was in fact viewed as a difficulty in removing water from the product [79]. When the droplet surface is saturated with free water (i.e. 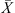 is high), the relative activation energy and hence the difficulty in removing the free moisture is expected to be very small (close to zero). The relative activation energy gradually increases when the droplet’s moisture content is reduced during drying. At the zero free moisture content (i.e.
is high), the relative activation energy and hence the difficulty in removing the free moisture is expected to be very small (close to zero). The relative activation energy gradually increases when the droplet’s moisture content is reduced during drying. At the zero free moisture content (i.e.  ), ΔE
v
/ΔE
v,b is expected to be unity.
), ΔE
v
/ΔE
v,b is expected to be unity.
Before simulating the spray drying process, it is essential to know the material’s relative activation energy profiles that correlate relative activation energy with the product’s average moisture content (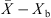 ) and thus allow estimating the average drying flux as a function of drying time. This relative activation energy profile was considered as a characteristic behavior (or fingerprint) of individual materials. The relative activation energy is mainly influenced by the composition of materials and the initial moisture contents [79]. The relative activation energy profiles for skim milk concentrates of different initial moisture contents are shown in Figure 1. For skim milk having 20 and 30 wt% (all dry basis) initial solids contents, the relative activation energy profiles were evaluated using weight loss and temperature data directly from the experimental work and equations (1) and (2) [17, 77], while for 40 wt% and higher solid concentrations these profiles were approximated using a method shown by Patel et al. [79]. A comparison of these relative activation energy curves in Figure 1 provides an insight for using an appropriate fingerprint. Mathematical equations describing the relative activation energy for 20, 30, 40, and 50 wt% (all dry basis) skim milk droplets are reported in Table I. The parameter ΔE
v,b can be calculated using the relative humidity (ρ
v,b/ρ
v,sat) and temperature (T
b) of hot air
) and thus allow estimating the average drying flux as a function of drying time. This relative activation energy profile was considered as a characteristic behavior (or fingerprint) of individual materials. The relative activation energy is mainly influenced by the composition of materials and the initial moisture contents [79]. The relative activation energy profiles for skim milk concentrates of different initial moisture contents are shown in Figure 1. For skim milk having 20 and 30 wt% (all dry basis) initial solids contents, the relative activation energy profiles were evaluated using weight loss and temperature data directly from the experimental work and equations (1) and (2) [17, 77], while for 40 wt% and higher solid concentrations these profiles were approximated using a method shown by Patel et al. [79]. A comparison of these relative activation energy curves in Figure 1 provides an insight for using an appropriate fingerprint. Mathematical equations describing the relative activation energy for 20, 30, 40, and 50 wt% (all dry basis) skim milk droplets are reported in Table I. The parameter ΔE
v,b can be calculated using the relative humidity (ρ
v,b/ρ
v,sat) and temperature (T
b) of hot air (2)
(2)
 |
Figure 1. Relative activation energy profiles to be used in the REA for the drying of skim milk of 20, 30, 40, 50, 55 and 60 (all wt%, dry basis) initial solids contents. |
Relative activation energy correlations for the air drying of skim milk.
Mass-transfer coefficient (h
m) in equation (1) can be estimated using the following equations: (3)
(3)
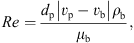 (4)
(4)
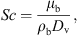 (5)where Sh is the Sherwood number, d
p (m) is the droplet’s diameter, D
v (m2·s−1) is the air-moisture diffusivity, Re is the Reynolds number, Sc is the Schmidt number, ρ
b (kg·m−3) and μ
b (Pa·s) are the density and viscosity of bulk gas, respectively, and v
p and v
b are the velocities of the droplet and bulk gas, respectively. Correlations to estimate various thermo-physical properties are listed in Appendix I.
(5)where Sh is the Sherwood number, d
p (m) is the droplet’s diameter, D
v (m2·s−1) is the air-moisture diffusivity, Re is the Reynolds number, Sc is the Schmidt number, ρ
b (kg·m−3) and μ
b (Pa·s) are the density and viscosity of bulk gas, respectively, and v
p and v
b are the velocities of the droplet and bulk gas, respectively. Correlations to estimate various thermo-physical properties are listed in Appendix I.
3.2. Mathematical equations
3.2.1. Heat balance
The temperature profile of a product can be evaluated using the following heat-transfer model: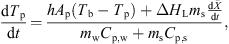 (6)where h (W·m−2·K−1) is the convective heat-transfer coefficient, ΔH
L (J·kg−1) is the latent heat of vaporization, and C
p,w and C
p,s (J·kg−1·K−1) are the specific heat capacities of water and solids, respectively. The heat-transfer coefficient, h, can be estimated from the following Ranz-Marshall correlation:
(6)where h (W·m−2·K−1) is the convective heat-transfer coefficient, ΔH
L (J·kg−1) is the latent heat of vaporization, and C
p,w and C
p,s (J·kg−1·K−1) are the specific heat capacities of water and solids, respectively. The heat-transfer coefficient, h, can be estimated from the following Ranz-Marshall correlation: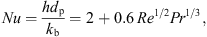 (7)where Pr is the Prandtl number that can be calculated from
(7)where Pr is the Prandtl number that can be calculated from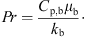 (8)
(8)
Temperature gradients across the droplet can be assessed using a method proposed by Patel and Chen [77]. If the temperature gradients are small or exist only for a short drying period, the assumption of uniform temperature can be used when estimating the droplet’s average temperature profiles using equation (6) [77, 78].
The temperature profile of hot gas can be evaluated using the following heat balance [71]: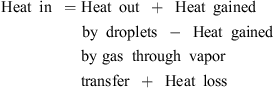
![$$ \dot{V}{\rho }_{\mathrm{b}}{H}_{\mathrm{b}}=\left[\dot{V}{\rho }_{\mathrm{b}}\left({H}_{\mathrm{b}}+\mathrm{d}{H}_{\mathrm{b}}\right)\right]+\left[h{A}_{\mathrm{p}}({T}_{\mathrm{b}}-{T}_{\mathrm{p}})\mathrm{\theta d}t\right]-\left[\frac{\mathrm{d}{m}_{\mathrm{w}}}{\mathrm{d}t}\left\{\Delta {H}_{\mathrm{L}}+{C}_{\mathrm{p},\mathrm{v}}\left({T}_{\mathrm{b}}-{T}_{\mathrm{p}}\right)\right\}\mathrm{\theta d}t\right]+\left[U(\pi {D}_{\mathrm{e}}\mathrm{d}l)({T}_{\mathrm{b}}-{T}_{\mathrm{\infty }})\right], $$](/articles/dst/full_html/2010/02/dst0979/dst0979-eq14.gif) (9)where
(9)where 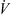 (m3·s−1) is the volumetric gas-flow rate, H
b (J·kg−1) is the enthalpy of gas, U (W·m−2·K−1) is the overall heat-transfer coefficient for heat loss, D
e (m) is the effective dryer diameter (the arithmetic average of inner and outer diameters) and T
∞
(K) is the room temperature. The enthalpy of hot air (H
b) can be estimated using [59]
(m3·s−1) is the volumetric gas-flow rate, H
b (J·kg−1) is the enthalpy of gas, U (W·m−2·K−1) is the overall heat-transfer coefficient for heat loss, D
e (m) is the effective dryer diameter (the arithmetic average of inner and outer diameters) and T
∞
(K) is the room temperature. The enthalpy of hot air (H
b) can be estimated using [59]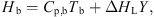 (10)where C
p,b (J·kg−1·K−1) and Y (kg·kg−1, dry basis) are the specific heat capacity and absolute humidity of hot air. The specific heat of humid air can be estimated using the following equation:
(10)where C
p,b (J·kg−1·K−1) and Y (kg·kg−1, dry basis) are the specific heat capacity and absolute humidity of hot air. The specific heat of humid air can be estimated using the following equation: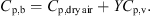 (11)
(11)
Using equations (9–11), the following heat-balance model can be derived to evaluate the air temperature profiles within the dryer:![$$ \dot{V}{\rho }_{\mathrm{b}}{C}_{\mathrm{p},\mathrm{b}}\frac{\mathrm{d}{T}_{\mathrm{b}}}{\mathrm{d}l}=\frac{\mathrm{\theta }}{{v}_{\mathrm{p}}}\left[\frac{\mathrm{d}{m}_{\mathrm{w}}}{\mathrm{d}t}\left\{\Delta {H}_{\mathrm{L}}+{C}_{\mathrm{p},\mathrm{v}}\left({T}_{\mathrm{b}}-{T}_{\mathrm{p}}\right)\right\}-h{A}_{\mathrm{p}}\left({T}_{\mathrm{b}}-{T}_{\mathrm{p}}\right)\right]-\dot{V}{\rho }_{\mathrm{b}}\left(\Delta {H}_{\mathrm{L}}+{C}_{\mathrm{p},\mathrm{v}}{T}_{\mathrm{b}}\right)\frac{\mathrm{d}Y}{\mathrm{d}l}-\left[U(\pi {D}_{\mathrm{e}})({T}_{\mathrm{b}}-{T}_{\mathrm{\infty }})\right]. $$](/articles/dst/full_html/2010/02/dst0979/dst0979-eq18.gif) (12)
(12)
3.2.2. Mass balance
Similar to heat balance, the following mass balance equation can be used to evaluate the absolute gas humidity profile inside the drying chamber: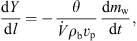 (13)where l (m) is the dryer’s axial height. The water evaporation rate dm
w/dt can be calculated from equation (1).
(13)where l (m) is the dryer’s axial height. The water evaporation rate dm
w/dt can be calculated from equation (1).
3.2.3. Momentum balance
The axial velocity profile of droplets/particles can be estimated using the following momentum balance equation:![$$ \frac{\mathrm{d}{v}_{\mathrm{p}}}{\mathrm{d}t}=\left[\left(\frac{{\rho }_{\mathrm{p}}-{\rho }_{\mathrm{b}}}{{\rho }_{\mathrm{p}}}\right)g-\left\{\frac{0.75{C}_{\mathrm{D}}{\rho }_{\mathrm{b}}}{{d}_{\mathrm{p}}{v}_{\mathrm{p}}}({v}_{\mathrm{p}}-{v}_{\mathrm{b}}{)}^2\right\}\right], $$](/articles/dst/full_html/2010/02/dst0979/dst0979-eq20.gif) (14)where C
D is the drag coefficient. For 0.5 < Re < 1000, C
D can be estimated from the following empirical correlation [21]:
(14)where C
D is the drag coefficient. For 0.5 < Re < 1000, C
D can be estimated from the following empirical correlation [21]: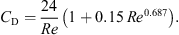 (15)
(15)
It is often important to estimate the initial velocity of the droplet to use as an input parameter to the simulation tool. For a pressure nozzle, the initial droplet velocity can be calculated by the following equation [59]: (16)where D
C (m) is the inlet channel (pipe) diameter (internal), A
C (m2) is the channel surface area,
(16)where D
C (m) is the inlet channel (pipe) diameter (internal), A
C (m2) is the channel surface area,  (m3·s−1) is the volumetric-flow rate of liquid concentrate, D
O (m) is the orifice diameter and b (m) is the liquid jet thickness at the orifice.
(m3·s−1) is the volumetric-flow rate of liquid concentrate, D
O (m) is the orifice diameter and b (m) is the liquid jet thickness at the orifice.
3.2.4. Shrinkage model
Modeling of a drying process requires a shrinkage model to estimate the change in the droplet’s diameter because the evaporation of water from the droplets makes them shrink. This shrinkage effect has a direct influence on the physical quality of the end products [43, 75]. Different models such as a perfect (or ideal) shrinkage model, a receding interface model and empirical (linear or non-linear) shrinkage models were reported in the literature to estimate the transient change in the diameter during drying [46, 54, 82, 89, 91, 98, 104]. Receding interface models assume that the droplets shrink only during the constant drying-rate period [46]. The formation of a solid crust during the falling-rate period is likely to restrict a shrinkage behavior. The perfect shrinkage and empirical models have widely been used in the literature because they are straightforward to incorporate into 1-D simulation tools. Selection of a shrinkage model should be based on how well these models are validated for specific materials under given drying conditions.
The perfect (ideal) shrinkage model, which is the simplest and possibly the most frequently used approach, assumes that the change in droplet diameter is proportional to the quantity of water removed from the droplets during drying [70]. Empirical models have also been used since they appear to provide higher accuracy in many studies [54–56]. For instance, Lin and Chen [54] used the following linear empirical model to estimate the change in diameter during the drying of skim milk droplets: (17)where parameter β is the empirical coefficient that is reported to be 0.59 and 0.69 for 20 and 30 wt% skim milk droplets [54]. Since the accurate values of β for the drying of higher initial solids concentrations skim milk are not yet reported, the ideal shrinkage model was used for simulation runs in this study.
(17)where parameter β is the empirical coefficient that is reported to be 0.59 and 0.69 for 20 and 30 wt% skim milk droplets [54]. Since the accurate values of β for the drying of higher initial solids concentrations skim milk are not yet reported, the ideal shrinkage model was used for simulation runs in this study.
The initial “representative” droplet diameter (d
p,0) in equation (17) can be estimated using the known atomizer parameters and the corresponding correlations published in the literature. For a pressure nozzle, the following correlation has widely been used [59]:![$$ {D}_{\mathrm{3,2}}=286\left(0.0254\enspace {D}_{\mathrm{O}}+0.17\right)\mathrm{exp}\left[\frac{39}{{v}_{\mathrm{p},0}}-0.00313\frac{\dot{V}}{{A}_{\mathrm{C}}}\right], $$](/articles/dst/full_html/2010/02/dst0979/dst0979-eq25.gif) (18)where D
3/2 (m) is the Sauter mean diameter that can be used as the initial “representative” droplet diameter to conduct simulation.
(18)where D
3/2 (m) is the Sauter mean diameter that can be used as the initial “representative” droplet diameter to conduct simulation.
3.2.5. Equilibrium moisture isotherm
It is essential to estimate equilibrium moisture contents (X
b) when using the REA to simulate drying processes. For different materials, different equilibrium moisture isotherms may be used to estimate X
b. The Guggenheim-Anderson-de Boer (GAB) model, which has been fitted at elevated temperatures (up to 90 °C) and over a wide range of relative humidity (up to 100%) conditions, can be used to calculate X
b of skim milk droplets [57]: (19)where C, K and m
0 are three parameters of the model and a
w is the water activity. These parameters were presented for skim milk using the following correlations [57]:
(19)where C, K and m
0 are three parameters of the model and a
w is the water activity. These parameters were presented for skim milk using the following correlations [57]: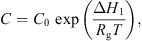 (20)
(20)
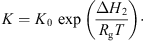 (21)
(21)
Here, C 0 and K 0 are fitting parameters, ΔH 1 and ΔH 2 (J·mol−1) are the enthalpies of water sorption, R (J·mol−1·K−1) is the universal gas constant and T (K) is the absolute temperature. Parameters m 0, C 0, K 0, ΔH 1 and ΔH 2 for skim milk were reported to be 0.06156, 0.001645, 5.71, 24 831 and −5118, respectively, by Lin et al. [55].
3.2.6. Product quality parameters
Density, glass-transition temperature and insolubility index are a few parameters of interest from the quality point of view. The true density profile of a particle can be estimated using the densities of solids and water. Since the water content profile of the particle is known from the drying kinetics model, the density profile can be estimated using mass fractions and densities of water and solids. Alternatively, the particle density can be predicted using the following equation: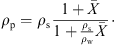 (22)
(22)
Glass-transition temperature and insolubility index are frequently used now to optimize process conditions to ensure that the product is non-sticky and has a good solubility. The first “spray drying” stage has however a large influence on these product properties, and it is advisable to know them beforehand. The glass-transition temperature (T
g) is a characteristic property of an amorphous component of materials and can be related to the stickiness behavior of powders during processing and storage. The Gordon-Taylor equation that seems to account for the water content effect can be used to estimate T
g of the solids-water mixture containing single or multiple solutes [1–3, 12, 29, 90, 96]: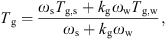 (23)where k
g is the solid-water (binary) constant, T
g,s and T
g,w are the glass-transition temperatures of solids and water, and ω
s and ω
w are the mass fractions of solids and water, respectively. T
g of skim milk solids (3 wt% moisture, dry basis) and water were reported to be 72 and −137 °C, respectively [13]. The parameter k
g has to be obtained from independent experiments [8]. It is often accepted that T
g profiles of skim milk droplets may be approximated by T
g of anhydrous lactose (101 °C) with a corresponding k
g of 7.4 [47, 69].
(23)where k
g is the solid-water (binary) constant, T
g,s and T
g,w are the glass-transition temperatures of solids and water, and ω
s and ω
w are the mass fractions of solids and water, respectively. T
g of skim milk solids (3 wt% moisture, dry basis) and water were reported to be 72 and −137 °C, respectively [13]. The parameter k
g has to be obtained from independent experiments [8]. It is often accepted that T
g profiles of skim milk droplets may be approximated by T
g of anhydrous lactose (101 °C) with a corresponding k
g of 7.4 [47, 69].
Solubility or insolubility index is another important property of dairy/food powders and usually considered as a post-drying property [65]. This property is often used by commercial milk powder manufacturers as a criterion to indicate the quality of milk powders. The insolubility index is an indicator of the presence of insoluble materials in the particle/powder and the ability of powder to dissolve in the solvent (water, milk, etc.) [9]. The rate of insoluble material formation during drying mainly depends on the protein contents of feed, the drying conditions and the temperature and moisture content profiles of the droplets. Straatsma et al. [94] proposed a zero-order kinetic model to determine the insolubility index of skim milk powders assuming that the insoluble material forms only when the particle moisture content is between 10 and 30 wt% (dry basis). The rate of insoluble material formation (r
isi) was described by Straatsma et al. [94] using the following empirical equation: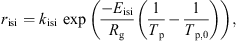 (24)where k
isi and E
isi are the kinetic constants at a reference temperature, and T
p and T
p,0 are the product temperature (K) and reference temperature (K), respectively. Straatsma et al. [94] evaluated constants k
isi = 0.054 mL·s−1 and E
isi = 2.7 × 105 J·mol−1 at T
0 = 348 K for skim milk powders. Since a qualitative model to show the effect of the moisture on the rate of insoluble material formation is not available to date, this idealistic kinetic model may provide “indicative” trends within the limited operating range.
(24)where k
isi and E
isi are the kinetic constants at a reference temperature, and T
p and T
p,0 are the product temperature (K) and reference temperature (K), respectively. Straatsma et al. [94] evaluated constants k
isi = 0.054 mL·s−1 and E
isi = 2.7 × 105 J·mol−1 at T
0 = 348 K for skim milk powders. Since a qualitative model to show the effect of the moisture on the rate of insoluble material formation is not available to date, this idealistic kinetic model may provide “indicative” trends within the limited operating range.
Other product quality parameters such as the rate of deactivation of bioactive substances (e.g. enzymes and vitamins) and their residual activity in the final products may also be estimated by incorporating appropriate mathematical models into 1-D simulation tools.
4. DEVELOPMENT OF A SPREADSHEET-BASED 1-D SIMULATION TOOL
In this example, a Microsoft Excel spreadsheet was used as a process calculation tool to simultaneously solve all the formulated equations and build a 1-D simulation spray drying software. A first-order finite difference method was used to solve mass-, heat- and momentum-transfer differential equations by following time integration. At each time step, a droplet travels a small distance (dh) in the dryer, thus dividing the dryer into many dryer “slices”. All the droplets in each dryer slice were considered to experience the identical conditions, thus having the same thermo-physical properties. The total number of droplets θ inside the dryer was estimated using the flow rate of concentrate and a representative droplet diameter (i.e. total droplets per second = total volumetric flow per second/volume of a single droplet).
The Excel spreadsheet was divided into three main parts where specific calculations were performed using a time interval of 0.005 s. The first part of the spreadsheet defines various inputs of spray drying processes. These inputs are absolute humidity, flow rate and temperature of inlet gas streams (i.e. main hot gas, cooling gas and gas with fines recycle) as well as temperature, flow rate and solids concentration of liquid feed, the dryer’s dimensions (diameter and height) and the representative diameter and velocity of the droplets. The second part of this 1-D tool calculates all required thermo-physical, chemical, transport and equilibrium properties of vapor, water, dry air and liquid feed including heat capacity, density, viscosity, thermal conductivity, latent heat of vaporization, partial vapor pressure, saturated vapor pressure and drag coefficient. These properties were time-dependent and varied along the axial distance in the drying chamber. The third part of the simulation tool handles with the drying kinetics of liquid feed and calculates a product’s physical properties such as density, moisture content, size, T g, solubility index, water activity, equilibrium moisture content, heat- and mass-transfer coefficients, drying rate and the distance travelled by the droplets at each time step.
Simulation for integrated fluid-bed drying was also combined with first-stage drying. Several important parameters after first and second drying stages were predicted and compared with experimental measurements. Synchronization of first-stage drying and fluid-bed drying of individual particles is a challenge although it is possible to combine them by introducing several simplifications. In this study, the fluid-bed dryer was treated as a well-mixed reactor. The detailed kinetic profiles of the product in the fluid-bed dryer were not projected. Drying kinetics profiles are reported in this paper only for first-stage drying in order to highlight the pros and cons of the 1-D simulation tool developed at the Clayton Campus of Monash University in Australia.
A few assumptions were used during simulation. These assumptions are:
-
A spray dryer was treated as a plug-flow reactor having a co-current flow.
-
The droplets were considered as spheres of a binary mixture (solids and water).
-
All the droplets in a specific dryer “slice” have identical size, shape and properties.
-
A perfect shrinkage model was considered reasonable to estimate shrinkage behavior.
-
The initial “representative” diameter and velocity can be estimated using appropriate empirical correlations available in the literature for individual atomizers [59].
5. SPRAY DRYING TRIALS ON A PILOT-SCALE MULTI-STAGE DRYER
To compare predicted parameters and study their trends, spray drying trials were performed at the Bionov pilot plant (Rennes, France). The evaporation capacity of this dryer was in the range of 70–100 kg water per hour. An internal static fluid-bed dryer and an external vibro fluid-bed dryer were used for final drying and agglomeration of powders. In this plant, the exhaust air stream is drawn out from the ceiling of the drying chamber to a set of two cyclones where fine particles are collected and returned to the top of the drying chamber. The diameter of the cylindrical chamber was 2 m, while the total height of this dryer was 3.9 m. Schematic layouts of this drying plant are presented by Bimbenet et al. [10] and not repeated here. A single pressure nozzle was used to spray liquid concentrates of known initial solids contents. Required operating and feed parameters were either recorded from a control panel board in the control room or measured directly from the plant wherever possible. The heat loss through the dryer surface was estimated to be ~ 2.5% of the total heat input. This heat loss was taken into account when estimating air temperature profiles. Three trials were performed using skim milk concentrates of 20 and 40 wt% solids contents. Inlet feed and operating conditions for these three trials are presented in Table II.
Inlet conditions for skim milk drying trials.
“Mixed air” in Table II indicates the total mixed air (hot air, cooling air around pressure nozzle and air coming in with fines) that is available to a spray of droplets near atomization zone. Temperature of mixed air was not measured during the spray drying trials but it was calculated using the relevant enthalpy of each air stream (excluding the hot air stream entering through static fluid-bed dryer). This means (25)where
(25)where 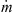 (kg·h−1) and H (kJ·kg−1) are the mass-flow rate and enthalpy of individual air streams. As an example, H
total of mixed air during skim milk trial 1 would be (see Tab. II for humidity, temperature and flow rate values)
(kg·h−1) and H (kJ·kg−1) are the mass-flow rate and enthalpy of individual air streams. As an example, H
total of mixed air during skim milk trial 1 would be (see Tab. II for humidity, temperature and flow rate values)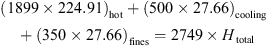

Temperature of this mixed air with enthalpy of 164 kJ·kg−1 and absolute humidity of 1 g·kg−1 was calculated to be 160.4 °C. This mixed air temperature was used in the 1-D tool as an initial air temperature.
6. RESULTS AND DISCUSSION
Detailed profiles and trends of important feed and gas parameters are predicted in this section using the 1-D simulation tool. Predictions of the 1-D tool are compared with experimental measurements and predictions of SD2P® software wherever possible. Figure 2a demonstrates the air temperature profiles estimated using the 1-D tool. The hot region within the dryer can be identified using these profiles. Overall outlet air temperatures predicted by the 1-D tool and SD2P® are presented in Figure 2b. To study the trend of prediction using three drying trials, measured outlet air temperatures are also reported in Figure 2b. Results indicate that the trends of prediction using both the software were similar to the measured outlet air temperatures (see Fig. 2b). When compared with measured outlet air temperatures, the average and maximum relative differences were estimated to be ~ 4.2% and 7.9% with the 1-D tool, and 1.7% and 2.0% with SD2P®. Both predictive tools slightly overestimated the outlet air temperatures.
 |
Figure 2. (a) Air temperature profiles predicted by the 1-D simulation tool and (b) outlet air temperatures from drying trials, 1-D simulation tool and SD2P® software. |
Figure 3a presents the air humidity profiles predicted by the 1-D tool. These air humidity and temperature profiles may be used to avoid stickiness and wall deposition issues. The trend of predictions using the 1-D tool and SD2P® and the measured outlet air humidity are shown in Figure 3b. It was observed that the outlet air humidity was somewhat overpredicted by the 1-D tool and SD2P®. Average and maximum relative errors in predictions by the 1-D tool were 10.8% and 17.4%, respectively, while these errors for SD2P® were ~ 6.3% and 9.7%, respectively. It was further observed that the air humidity after first-stage drying tends to be slightly higher than the outlet air humidity.
 |
Figure 3. (a) Air humidity profiles predicted by the 1-D simulation tool and (b) outlet air humidity from drying trials, 1-D simulation tool and SD2P® software. |
Powder moisture content profiles during the first-stage drying are predicted using the 1-D tool and illustrated in Figure 4a. These profiles help in identifying the dryer zones where the majority of the water is removed. Powder moisture contents after both first-stage and fluidized-bed drying (see Fig. 4b) are also estimated. The final moisture contents of the powder (i.e. after external fluid-bed drying) were measured and reported to be 0.044 kg·kg−1 (dry basis) for all three drying trials. Because the SD2P® software presumes the average moisture contents of the powder after the first drying stage and fluidized-bed drying, the predicted moisture contents by the 1-D tool could not be compared with the predictions of SD2P®. It should be noted that SD2P® used the final moisture content as an input parameter to the model while the 1-D tool “predicts” the powder’s moisture contents throughout drying, and thus allows the estimation of other moisture content-based product properties such as glass-transition temperature, insolubility index and residual activity of bioactive components.
 |
Figure 4. (a) Powder moisture content profiles predicted by the 1-D simulation tool and (b) outlet powder moisture contents from drying trials, 1-D simulation tool and SD2P® software. |
Figure 4b shows that the powder’s moisture content was overpredicted for the second drying trial while it was underpredicted for the third drying trial when using the 1-D tool. Average powder moisture contents after first-stage drying should be in the range of 0.07–0.09 kg·kg−1 (dry basis) based on overall moisture balance calculations. The error in prediction may be due to the inclusion of various assumptions (such as co-current axial flow, no droplet size distribution, spherical droplets, no agglomeration, no droplet-droplet or droplet-wall interactions, no gas recirculation within the chamber and ignorance of fines near the atomization zone) and various approximate models (such as ideal shrinkage, empirical correlation for estimating the droplet size and Ranz-Marshall correlations). It is expected to have a certain degree of errors due to these approximations.
Variations in the feed/air parameters during spray drying operations may also introduce errors in recording drying/gas parameters and hence during spray drying simulation. For instance, a variation in the feed-flow rate during the pilot-scale drying trials was recorded to be ~ ± 3.0–8.0 L·h−1. A variation in the gas-flow rate during drying was more noticeable. Therefore, it was often difficult to record accurate gas and feed parameters to enter in the simulation program. Other spray drying software products available in the market which require inlet/outlet gas and feed parameters as inputs to the simulation tool may also face this challenge.
During spray drying experiments, fines were returned at the top of the drying chamber and mixed with fresh droplets. However, the return of fines was not considered during heat and mass balances by the 1-D simulation software. In fact, fines returns could be as high as 60–80% of the total powder produced after first-stage drying [40]. Such a high fraction of fines may have a certain influence (not necessarily significant) on the overall heat-mass balances and average drying flux of fresh droplets. The interactions of fresh droplets with the fines near the atomization zone, their impact on the average drying flux and the modeling for these droplet phenomena have remained a challenge. Nevertheless, the trend of product moisture contents delivered by the 1-D simulation approach appeared to be correct, and these trends may be used to study the sensitivity of various drying/feed parameters.
A higher accuracy may be achieved by tuning the empirical coefficients of several mathematical models for specific products or process conditions. Another way to improve the accuracy of prediction may be to incorporate an adjustment parameter or an air-droplets mixing coefficient into the model. However, it is not clear yet how and where to introduce adjustment parameters during spray drying simulations.
Particle velocity and gas velocity profiles are predicted by the 1-D tool and presented in Figure 5. The initial “representative” axial droplet velocity was estimated to be ~ 31.5, 29.5, and 35.4 m·s−1 for drying trials 1, 2, and 3. The inlet gas velocity was approximated around 6.0 m·s−1. The real dryer geometry was considered during simulation. It was observed that both the particle and gas velocities slightly went up at the bottom of the drying chamber due to the conical shape of the chamber. Particle residence time during the first-stage drying, assuming co-current parallel flow, was in the range of 3.5–5.0 s for the reported drying trials.
 |
Figure 5. Droplet and air velocity profiles predicted by the 1-D simulation tool. |
Figure 6a demonstrates glass-transition temperature (T g) and product temperature (T p) profiles. T g for skim milk powder was estimated using T g of anhydrous lactose as done by Langrish [47]. T g values after first-stage drying corresponding to the drying trials 1, 2, and 3 (product moisture contents of 6.3, 16.6, and 2.4 wt%) were 64.2, −19.8, and 100.1 °C, respectively. Respective T p–T g values after first-stage drying were approximately 20, 95, and −22 °C. These predictions show that the product may be slightly sticky for trial 1, very sticky for trial 2, and non-sticky for trial 3. The error of prediction in estimating the product’s moisture concentrations directly reflected in the T g predictions. Accurate T g profiles can be helpful in drawing safe drying regime maps and taking decisions on tuning inlet/outlet gas temperature/humidity to produce non-sticky products with minimum wall deposition.
 |
Figure 6. (a) Glass-transition temperature (T g) and product temperature profiles and (b) insolubility index profiles estimated by the 1-D simulation tool for the skim milk drying trials. |
Insolubility index profiles are also predicted by the 1-D tool and reported in Figure 6b. One should be careful when reading the insolubility index when predicting them using the model (equation 24) used in this study. The model assumed that the insoluble material forms only when the product moisture content was between 10 and 30 wt%. Based on this assumption, the insolubility index for the drying trials 1, 2 and 3 was ~ 1.09, 0.07, and 0.14 mL (at 10 wt% powder moisture). The effect of the product’s temperature profiles has been reflected on the insolubility index. Experimental solubility data and SD2P® predictions for this property are not available. The insolubility index data during first-stage drying may help in giving a rough estimate on how much insoluble material forms during the subsequent drying stages and storage.
It was noticed during this case study that the trends of prediction using the 1-D simulation tool were similar to experimental data recorded from the plant. The 1-D tool also helped in observing the variations in product and gas properties upon changing inlet feed and air parameters. Despite introducing several simplifications in this study to make the 1-D tool simpler and faster, the correct trends of important product and gas properties were obtained. The absolute errors of prediction by the 1-D tool for the drying trials conducted on the pilot-scale dryer were in the range of 3–17%. These errors may be minimized by modifying heat and mass balances that closely resemble real spray drying trials, by tuning several empirical parameters and by introducing an adjustment coefficient in the model.
It should be noted that the input parameters to the 1-D simulation tool built for this study and SD2P® software are quite different. SD2P® requires the outlet moisture content and outlet air temperature as input parameters in order to calculate the inlet air temperature for achieving the presumed moisture content. The 1-D simulation tool requires all the inlet conditions to the dryer as inputs to the simulation and predicts important parameters at the outlet of the drying chamber. To achieve the desired outlet moisture content or outlet gas temperature with the 1-D tool, the input parameters should be changed until the desired outlet conditions are obtained. Nevertheless, both the 1-D simulation tool and SD2P® software are quite useful to perform simulations for spray drying operations. Several important pros and cons of the 1-D simulation approach are mentioned in the next section.
7. PROS AND CONS
7.1. Pros of 1-D simulation approach
-
The first important advantage of a 1-D simulation tool with an Excel spreadsheet platform is that fast calculations can be performed. Product and process parameters can be predicted and their trends can be projected within a few seconds unlike multi-dimensional simulation approaches that may require hours, days or even weeks to evaluate valuable information for industrial-scale drying operations. Spreadsheet-based 1-D software is becoming an indispensible tool for process and plant engineers because of the ease of use and the saving of time and resources.
-
1-D approach requires only a few inlet feed and gas parameters as inputs to the simulation program.
-
1-D tool evaluates the product’s temperature and moisture content throughout drying which allow for predicting the product’s quality parameters not only at the dryer’s inlet and outlet but also within the dryer chambers.
-
Safe drying regime maps can be prepared to produce non-sticky products, to determine the extent of particle crystallinity required for product stability and to minimize wall deposition.
-
1-D simulation approach can be a great means to track the consequences of changes in process and feed parameters on important product quality parameters, energy consumptions and process efficiencies. For instance, if the inlet air humidity to the dryer is changing in a rainy season, it is fast and straightforward to decide what changes should be made to inlet air temperature or inlet feed-flow rates or other parameters to keep the product’s moisture content consistent at the dryer outlet. Furthermore, it can be quickly estimated what inlet air temperatures should be used for any variation in the feed’s initial solids concentrations. This information can be presented using simple graphs or tables and provided to the plant operators.
-
Recently, Patel and Chen [76] demonstrated the ability of estimating surface properties of particles throughout drying using the 1-D simulation tool and the REA. Previously, the surface properties of products were estimated using a diffusion-based drying kinetics approach or a receding interface approach that required using much more complex process calculation tools such as MATLAB and FlexPDE.
7.2. Cons of 1-D simulation approach
-
Several dryer geometries involve the recirculation of particles within the drying chamber, the recirculation of humid air to the ceiling of the chamber and the fines return to the dryer. At this stage the 1-D approach does not account for these phenomena and cannot predict gas distribution within the chamber, droplet/particle trajectories and gas-particles residence time data. 2-D and 3-D simulation approaches may be helpful to handle these spray drying phenomena in order to study these phenomena in more depth.
-
The 1-D simulation approach does not consider droplet-droplet interactions and droplet-particle interactions in the dryer which are common phenomena for real spray drying operations.
-
Simulation of the drying of agglomerated particles is also a challenge for the 1-D approach.
-
The 1-D approach requires several parameters from the laboratory-scale experiments prior to simulation if they are not known. These parameters include drying kinetics parameters (e.g. relative activation energy), shrinkage parameters, equilibrium moisture isotherm parameters and quality parameters (e.g. T g of anhydrous solids). Any errors in obtaining experimental data and validating associated mathematical models may have a certain influence on the accuracy of prediction by the 1-D simulation approach.
8. CONCLUSION
The 1-D simulation approach offers valuable information on operating parameters before production of powders. Moisture content and temperature-dependent product properties can be predicted at any locations in the dryer, thus giving an additional advantage over the “black box” approach. When a good understanding of the principles of spray drying and the characteristics of the particular plant in use is coupled with the information obtained by the predictive tools, sensible decisions can be made to avoid potential problems and to improve product quality and process efficiencies. The user of 1-D simulation tools should, however, be aware of the accuracy of prediction when taking decisions based on the trends/numbers provided by the 1-D tools. From the customer’s point of view, simulation software should be easy to use, of low cost and be readily available in the market. Predictive tools based on a 1-D simulation approach can be constructed using spreadsheet-based platforms like Excel which offer simplicity and cost-related benefits over other CFD- and MATLAB-based process calculation tools.
Acknowledgments
The authors gratefully acknowledge Dairy Innovation Australia Limited (Australia), the Geoffrey Gardiner Dairy Foundation (Australia), and l’Institut National de la Recherche Agronomique (France) for their financial and other support for this research. The authors also thank Dr. Martin Palmer from Dairy Innovation Australia Limited (Australia) for his valuable comments and suggestions on various technical aspects of this paper.
References
- Adhikari B., Howes T., Bhandari B.R., Troung V., Surface stickiness of drops of carbohydrate and organic acid solutions during convective drying: experiments and modeling, Dry. Technol. 21 (2003) 839–873. [CrossRef] [Google Scholar]
- Adhikari B., Howes T., Bhandari B.R., Troung V., Effect of addition of maltodextrin on drying kinetics and stickiness of sugar and acid-rich foods during convective drying: experiments and modelling, J. Food Eng. 62 (2004) 53–68. [CrossRef] [Google Scholar]
- Adhikari B., Howes T., Lecomte D., Bhandari B.R., A glass transition temperature approach for the prediction of the surface stickiness of a drying droplet during spray drying, Powder Technol. 149 (2005) 168–179. [Google Scholar]
- Aguerre R.J., Suarez C., Diffusion of bound water in starchy materials: application to drying, J. Food Eng. 64 (2004) 389–395. [CrossRef] [Google Scholar]
- Alamilla-Beltrán L., Chanona-Pérez J.J., Jiménez-Aparicio A.R., Gutiérrez-López G.F., Description of morphological changes of particles along spray drying, J. Food Eng. 67(2005) 179–184. [CrossRef] [Google Scholar]
- Ben-Yoseph E., Hartel R.W., Howling D., Three-dimensional model of phase transition of thin sucrose films during drying, J. Food Eng. 44 (2000) 13–22. [CrossRef] [Google Scholar]
- Bernard C., Broyart B., Vasseur J., Relkin P., Production of whey protein powders with controlled end-use properties, 15th International Drying Symposium, Budapest, Hungary, 2006. [Google Scholar]
- Bhandari B.R., Howes T., Implication of glass transition for the drying and stability of dried foods, J. Food Eng. 40 (1999) 71–79. [CrossRef] [Google Scholar]
- Bhandari B.R., Patel K.C., Chen X.D., Spray drying of food materials – process and product characteristics, in: Chen X.D., Mujumdar A.S. (Eds.), Drying Technologies in Food Processing, Blackwell Publishing, West Sussex, UK, 2008, 113–159. [Google Scholar]
- Bimbenet J.J., Schuck P., Roignant M., Brulé G., Méjean S., Heat balance of a multistage spray-dryer: principles and example of application, Lait 82 (2002) 541–551. [CrossRef] [EDP Sciences] [Google Scholar]
- Birchal V.S., Huang L., Mujumdar A.S., Passos M.L., Spray dryers: modeling and simulation, Dry. Technol. 24 (2006) 359–371. [CrossRef] [Google Scholar]
- Boonyai P., Bhandari B., Howes T., Stickiness measurement techniques for food powders: a review, Powder Technol. 145 (2004) 34–46. [CrossRef] [Google Scholar]
- Boonyai P., Bhandari B., Howes T., Measurement of glass-rubber transition temperature of skim milk powder by static mechanical test, Dry. Technol. 23 (2005) 1499–1514. [CrossRef] [Google Scholar]
- Bruce L.J., Okos M.R., Moisture diffusivity in pasta during drying, J. Food Eng. 17 (1992) 117–142. [CrossRef] [Google Scholar]
- Chen X.D., Heat-mass transfer and structure formation during drying of single food droplets, Dry. Technol. 22 (2004) 179–190. [CrossRef] [Google Scholar]
- Chen X.D., Moisture diffusivity in food and biological materials, Dry. Technol. 25 (2007) 1203–1213. [CrossRef] [Google Scholar]
- Chen X.D., Lin S.X.Q., Air drying of milk droplet under constant and time-dependent conditions, AIChE J. 51 (2005) 1790–1799. [CrossRef] [Google Scholar]
- Chen X.D., Patel K.C., Manufacturing better quality food powders from spray drying and subsequent treatments, Dry. Technol. 26 (2008) 1313–1318. [CrossRef] [Google Scholar]
- Chen X.D., Pirini W., Ozilgen M., The reaction engineering approach to modelling drying of thin layer of pulped kiwifruit flesh under conditions of small biot numbers, Chem. Eng. Process 40 (2001) 311–320. [CrossRef] [Google Scholar]
- Chen X.D., Xie G.Z., Fingerprints of the drying behaviour of particulate or thin layer food materials established using a reaction engineering model, Food Bioprod. Process 75 (1997) 213–222. [CrossRef] [Google Scholar]
- Crowe C.T., Sommerfeld M., Tsuji Y., Fundamentals of Gas-Particle and Gas-Droplet Flows, CRC Press, Boca Raton, USA, 1998. [Google Scholar]
- Dalmaz N., Ozbelge H.O., Eraslan A.N., Uludag Y., Heat and mass transfer mechanisms in drying of a suspension droplet: a new computational model, Dry. Technol. 25 (2007) 391–400. [CrossRef] [Google Scholar]
- Dolinsky A.A., High-temperature spray drying, Dry. Technol. 19 (2001) 785–806. [CrossRef] [Google Scholar]
- Doymaz I., Convective air drying characteristics of thin layer carrots, J. Food Eng. 61 (2004) 359–364. [CrossRef] [Google Scholar]
- Efremov G.I., Drying kinetics derived from diffusion equation with flux-type boundary conditions, Dry. Technol. 20 (2002) 55–66. [CrossRef] [Google Scholar]
- Efremov G.I., Kudra T., Calculation of the effective diffusion coefficients by applying a quasi-stationary equation for drying kinetics, Dry. Technol. 22 (2004) 2273–2279. [CrossRef] [Google Scholar]
- Ferrari G., Meerdink G., Walstra P., Drying kinetics for a single droplet of skim-milk, J. Food Eng. 10 (1989) 215–230. [CrossRef] [Google Scholar]
- Fletcher D.F., Guo B., Harvie D.J.E., Langrish T.A.G., Nijdam J.J., Williams J., What is important in the simulation of spray dryer performance and how do current CFD models perform?, Appl. Math. Model. 30 (2006) 1281–1292. [CrossRef] [Google Scholar]
- Foster K.D., Bronlund J.E., Paterson A.H.J., Glass transition related cohesion of amorphous sugar powders, J. Food Eng. 77 (2006) 997–1006. [CrossRef] [Google Scholar]
- Gauvin W.H., Katta S., Basic concepts of spray dryer design, AIChE J. 22 (1976) 713–724. [CrossRef] [Google Scholar]
- Gauvin W.H., Katta S., Knelman F.H., Drop trajectory predictions and their importance in the design of spray dryers, Int. J. Multiphas. Flow. 1 (1975) 793–816. [CrossRef] [Google Scholar]
- Groenewold C., Moser C., Groenewold H., Tsotsas E., Determination of single-particle drying kinetics in an acoustic levitator, Chem. Eng. J. 86 (2002) 217–222. [CrossRef] [Google Scholar]
- Guo B., Fletcher D.F., Langrish T.A.G., Simulation of the agglomeration in a spray using Lagrangian particle tracking, Appl. Math. Model. 28 (2004) 273–290. [CrossRef] [Google Scholar]
- Guo B., Langrish T.A.G., Fletcher D.F., Simulation of gas flow instability in a spray dryer, Chem. Eng. Res. Des. 81 (2003) 631–638. [CrossRef] [Google Scholar]
- Harvie D.J.E., Langrish T.A.G., Fletcher D.F., A computational fluid dynamics study of a tall-form spray dryer, Food Bioprod. Process. 80 (2002) 163–175. [CrossRef] [Google Scholar]
- Huang L., Kumar K., Mujumdar A.S., Use of computational fluid dynamics to evaluate alternative spray dryer chamber configurations, Dry. Technol. 21 (2003) 385–412. [Google Scholar]
- Huang L.X., Kumar K., Mujumdar A.S., A comparative study of a spray dryer with rotary disc atomizer and pressure nozzle using computational fluid dynamic simulations, Chem. Eng. Process. 45 (2006) 461–470. [CrossRef] [Google Scholar]
- Huang L.X., Mujumdar A.S., Simulation of an industrial spray dryer and prediction of off-design performance, Dry. Technol. 25 (2007) 703–714. [Google Scholar]
- Incropera F.P., DeWitt D.P., Fundamentals of Heat and Mass Transfer, 5th edn., John Wiley & Sons, New York, USA, 2002. [Google Scholar]
- Jeantet R., Ducept R., Dolivet A., Méjean S., Schuck P., Residence time distribution: a tool to improve spray-drying control, Dairy Sci. Technol. 88 (2008) 31–43. [CrossRef] [EDP Sciences] [Google Scholar]
- Jin Y., Chen X.D., Numerical study of the drying process of different sized particles in an industrial-scale spray dryer, Dry. Technol. 27 (2009) 371–381. [Google Scholar]
- Kastner O., Brenn G., Rensink D., Tropea C., The acoustic tube levitator – a novel device for determining the drying kinetics of single droplets, Chem. Eng. Technol. 24 (2001) 335–339. [CrossRef] [Google Scholar]
- Katekawa M.E., Silva M.A., On the influence of glass transition on shrinkage in convective drying of fruits: a case study of banana drying, Dry. Technol. 25 (2007) 1659–1666. [CrossRef] [Google Scholar]
- Ketelaars A.A.J., Pel L., Coumans W.J., Kerkhof P.J.A.M., Drying kinetics: a comparison of diffusion coefficients from moisture concentration profiles and drying curves, Chem. Eng. Sci. 50 (1995) 1187–1191. [CrossRef] [Google Scholar]
- Kieviet F.G., Van Raaij J., De Moor P.P.E.A., Kerkhof P.J.A.M., Measurement and modelling of the air flow pattern in a pilot-plant spray dryer, Chem. Eng. Res. Des. 75 (1997) 321–328. [CrossRef] [Google Scholar]
- Kuts P.S., Strumillo C., Zbicinski I., Evaporation kinetics of single droplets containing dissolved biomass, Dry. Technol. 14 (1996) 2041–2060. [CrossRef] [Google Scholar]
- Langrish T.A.G., Multi-scale mathematical modelling of spray dryers, J. Food Eng. 93 (2009) 218–228. [CrossRef] [Google Scholar]
- Langrish T.A.G., Kockel T.K., The assessment of a characteristic drying curve for milk powder for use in computational fluid dynamics modelling, Chem. Eng. J. 84 (2001) 69–74. [CrossRef] [Google Scholar]
- Langrish T.A.G., Kota K., A comparison of collision kernels for sprays from one and two-nozzle atomisation systems, Chem. Eng. J. 126 (2007) 131–138. [CrossRef] [Google Scholar]
- Langrish T.A.G., Williams J., Fletcher D.F., Simulation of the effects of inlet swirl on gas flow patterns in a pilot-scale spray dryer, Chem. Eng. Res. Des. 82 (2004) 821–833. [CrossRef] [Google Scholar]
- Leiterer J., Delißen F., Emmerling F., Thünemann A., Panne U., Structure analysis using acoustically levitated droplets, Anal. Bioanal. Chem. 391 (2008) 1221–1228. [CrossRef] [PubMed] [Google Scholar]
- Li Z., Kobayashi N., Determination of moisture diffusivity by thermo-gravimetric analysis under non-isothermal condition, Dry. Technol. 23 (2005) 1331–1342. [CrossRef] [Google Scholar]
- Li X., Zbicinski I., A sensitivity study on CFD modeling of cocurrent spray-drying process, Dry. Technol. 23 (2005) 1681–1691. [CrossRef] [Google Scholar]
- Lin S.X.Q., Chen X.D., Changes in milk droplet diameter during drying under constant drying conditions investigated using the glass-filament method, Food Bioprod. Process. 82 (2004) 213–218. [CrossRef] [Google Scholar]
- Lin S.X.Q., Chen X.D., A model for drying of an aqueous lactose droplet using the reaction engineering approach, Dry. Technol. 24 (2006) 1329–1334. [CrossRef] [Google Scholar]
- Lin S.X.Q., Chen X.D., The reaction engineering approach to modelling the cream and whey protein concentrate droplet drying, Chem. Eng. Process. 46 (2007) 437–443. [CrossRef] [Google Scholar]
- Lin S.X.Q., Chen X.D., Pearce D.L., Desorption isotherm of milk powders at elevated temperatures and over a wide range of relative humidity, J. Food Eng. 68 (2005) 257–264. [CrossRef] [Google Scholar]
- Madamba P.S., Driscoll R.H., Buckle K.A., The thin-layer drying characteristics of garlic slices, J. Food Eng. 29 (1996) 75–97. [Google Scholar]
- Masters K., Spray Drying Handbook, 5th edn., Longman Scientific & Technical, New York, USA, 1991. [Google Scholar]
- Meerdink G., Drying of Liquid Food Droplets: Enzyme Inactivation and Multicomponent Diffusion, Wageningen Agriculture University, Netherlands, 1993. [Google Scholar]
- Meerdink G., Riet K.V., Prediction of product quality during spray drying, Food Bioprod. Process. 73 (1995) 165–170. [Google Scholar]
- Menting L.C., Hoogstad B., Volatiles retention during the drying of aqueous carbohydrate solutions, J. Food Sci. 32 (1967) 87–90. [CrossRef] [Google Scholar]
- Mezhericher M., Levy A., Borde I., Heat and mass transfer of single droplet/wet particle drying, Chem. Eng. Sci. 63 (2008) 12–23. [CrossRef] [Google Scholar]
- Mezhericher M., Levy A., Borde I., Modeling of droplet drying in spray chambers using 2d and 3d computational fluid dynamics, Dry. Technol. 27 (2009) 359–370. [Google Scholar]
- Mistry V.V., Pulgar J.B., Physical and storage properties of high milk protein powder, Int. Dairy J. 6 (1996) 195–203. [CrossRef] [Google Scholar]
- Negiz A., Lagergren E.S., Cinar A., Mathematical models of cocurrent spray drying, Ind. Eng. Chem. Res. 34 (1995) 3289–3302. [Google Scholar]
- Nevers N.D., Physical and Chemical Equilibrium for Chemical Engineers, John Wiley & Sons, New York, USA, 2002. [Google Scholar]
- Oakley D.E., Bahu R.E., Computational modelling of spray dryers, Comp. Chem. Eng. 17 (1993) 493–498. [CrossRef] [Google Scholar]
- Ozmen L., Langrish T.A.G., Comparison of glass transition temperature and sticky point temperature for skim milk powder, Dry. Technol. 20 (2002) 1177–1192. [CrossRef] [Google Scholar]
- Parti M., Paláncz B., Mathematical model for spray drying, Chem. Eng. Sci. 29 (1974) 355–362. [CrossRef] [Google Scholar]
- Patel K.C., Production of uniform particles via single stream drying and new applications of the reaction engineering approach, Ph.D. Thesis, Monash University, Australia, 2009. [Google Scholar]
- Patel K.C., Chen X.D., Mathematical Modelling for Plug-Flow Spray Dryer, Chemeca 2004, Sydney, Australia, 2004. [Google Scholar]
- Patel K.C., Chen X.D., Prediction of spray-dried product quality using two simple drying kinetics models, J. Food Process Eng. 28 (2005) 567–594. [CrossRef] [Google Scholar]
- Patel K.C., Chen X.D., Sensitivity analysis of the reaction engineering approach to modeling spray drying of whey proteins concentrate, in: Chen G., Mujumdar A.S. (Eds.), The 5th Asia-Pacific Drying Conference, HKUST, Hong Kong, China, 2007, pp. 276–281. [CrossRef] [Google Scholar]
- Patel K.C., Chen X.D., Drying of aqueous lactose solutions in a single stream dryer, Food Bioprod. Process. 86 (2008) 185–197. [CrossRef] [Google Scholar]
- Patel K.C., Chen X.D., The reaction engineering approach to estimate surface properties of aqueous droplets during convective drying, in: Thorat B., Mujumdar A.S. (Eds.), International Drying Symposium 2008, Hyderabad, India, 2008, pp. 235–241 [Google Scholar]
- Patel K.C., Chen X.D., Surface-center temperature differences within milk droplets during convective drying and drying-based biot number analysis, AIChE J. 54 (2008) 3273–3290. [CrossRef] [Google Scholar]
- Patel K.C., Chen X.D., Kar S., The temperature uniformity during air drying of a colloidal liquid droplet, Dry. Technol. 23 (2005) 2337–2367. [CrossRef] [Google Scholar]
- Patel K.C., Chen X.D., Lin S.X.Q., Adhikari B., A composite reaction engineering approach to drying of aqueous droplets containing sucrose, maltodextrin (de6) and their mixtures, AIChE J. 55 (2009) 217–231. [CrossRef] [Google Scholar]
- Písecký J., Handbook of Milk Powder Manufacture, Niro A/S, Copenhagen, Denmark, 1997. [Google Scholar]
- Raghavan G.S.V., Tulasidas T.N., Sablani S.S., Ramaswamy H.S., A method of determination of concentration dependent effective moisture diffusivity, Dry. Technol. 13 (1995) 1477–1488. [CrossRef] [Google Scholar]
- Ratti C., Shrinkage during drying of foodstuffs, J. Food Eng. 23 (1994) 91–105. [CrossRef] [Google Scholar]
- Sano Y., Keey R.B., The drying of a spherical particle containing colloidal material into a hollow sphere, Chem. Eng. Sci. 37 (1982) 881–889. [CrossRef] [Google Scholar]
- Schadler N., Kast W., A complete model of the drying curve for porous bodies – Experimental and theoretical studies, Int. J. Heat Mass Transfer 30 (1987) 2031–2044. [CrossRef] [Google Scholar]
- Schiffter H., Lee G., Single-droplet evaporation kinetics, particle formation in an acoustic levitator. Part 1: Evaporation of water microdroplets assessed using boundary-layer and acoustic levitation theories, J. Pharm. Sci. 96 (2007) 2274–2283. [CrossRef] [PubMed] [Google Scholar]
- Schiffter H., Lee G., Single-droplet evaporation kinetics, particle formation in an acoustic levitator. Part 2: Drying kinetics and particle formation from microdroplets of aqueous mannitol, trehalose, or catalase, J. Pharm. Sci. 96 (2007) 2284–2295. [CrossRef] [PubMed] [Google Scholar]
- Schuck P., Dolivet A., Méjean S., Zhu P., Blanchard E., Jeantet R., Drying by desorption: a tool to determine spray drying parameters, J. Food Eng. 94 (2009) 199–204. [CrossRef] [Google Scholar]
- Schuck P., Roignant M., Brulé G., Davenel A., Famelart M.H., Maubois J.L., Simulation of water transfer in spray drying, Dry. Technol. 16 (1998) 1371–1393. [CrossRef] [Google Scholar]
- Seydel P., Blomer J., Bertling J., Modeling particle formation at spray drying using population balances, Dry. Technol. 24 (2006) 137–146. [CrossRef] [Google Scholar]
- Shrestha A.K., Howes T., Adhikari B.P., Bhandari B.R., Water sorption and glass transition properties of spray dried lactose hydrolysed skim milk powder, LWT – Food Sci. Technol. 40 (2007) 1593–1600. [CrossRef] [Google Scholar]
- Shulyak V.A., Izotova L.A., Shrinkage kinetics during convective drying of selected berries, Dry. Technol. 27 (2009) 495–501. [CrossRef] [Google Scholar]
- Sloth J., Kiil S., Jensen A.D., Andersen S.K., Jørgensen K., Schiffter H., Lee G., Model based analysis of the drying of a single solution droplet in an ultrasonic levitator, Chem. Eng. Sci. 61 (2006) 2701–2709. [CrossRef] [Google Scholar]
- Straatsma J., Van Houwelingen G., Steenbergen A.E., De Jong P., Spray drying of food products: 1. Simulation model, J. Food Eng. 42 (1999) 67–72. [CrossRef] [Google Scholar]
- Straatsma J., Van Houwelingen G., Steenbergen A.E., De Jong P., Spray drying of food products: 2. Prediction of insolubility index, J. Food Eng. 42 (1999) 73–77. [CrossRef] [Google Scholar]
- Strumillo C., Kudra T., Drying: Principles, Applications, and Design, Gordon and Breach Science Publishers, New York, USA, 1986. [Google Scholar]
- Truong V., Bhandari B.R., Howes T., Optimization of co-current spray drying process of sugar-rich foods, Part I. Moisture and glass transition temperature profile during drying, J. Food Eng. 71 (2005) 55–65. [Google Scholar]
- Verdurmen R.E.M., Menn P., Ritzert J., Blei S., Nhumaio G.C.S., Oslash Rensen T.S., Gunsing M., Straatsma J., Verschueren M., Sibeijn M., Schulte G., Fritsching U., Bauckhage K., Tropea C., Sommerfeld M., Watkins A.P., Yule A.J., Schonfeldt H., Simulation of agglomeration in spray drying installations: the edecad project, Dry. Technol. 22 (2004) 1403–1461. [Google Scholar]
- Viollaz P.E., Rovedo C.O., A drying model for three-dimensional shrinking bodies, J. Food Eng. 52 (2002) 149–153. [CrossRef] [Google Scholar]
- Walton D.E., The evaporation of water droplets. A single droplet drying experiment, Dry. Technol. 22 (2004) 431–456. [CrossRef] [Google Scholar]
- Woo M.W., Daud W.R.W., Mujumdar A.S., Talib M.Z.M., Hua W.Z., Tasirin S.M., Comparative study of droplet drying models for CFD modelling, Chem. Eng. Res. Des. 86 (2008) 1038–1048. [CrossRef] [Google Scholar]
- Woo M.W., Daud W.R.W., Mujumdar A.S., Wu Z., Talib M.Z.M., Tasirin S.M., Non-swirling steady and transient flow simulations in short-form spray dryers, Chem. Prod. Process Model. 4 (2009) 1–32. [Google Scholar]
- Woo M.W., Daud W.R.W., Tasirin S.M., Talib M.Z.M., Effect of wall surface properties at different drying kinetics on the deposition problem in spray drying, Dry. Technol. 26 (2008) 15–26. [Google Scholar]
- Wulsten E., Lee G., Surface temperature of acoustically levitated water microdroplets measured using infra-red thermography, Chem. Eng. Sci. 63 (2008) 5420–5424. [CrossRef] [Google Scholar]
- Yadollahinia A., Jahangiri M., Shrinkage of potato slice during drying, J. Food Eng. 94 (2009) 52–58. [CrossRef] [Google Scholar]
- Yarin A.L., Brenn G., Kastner O., Rensink D., Tropea C., Evaporation of acoustically levitated droplets, J. Fluid Mech. 399 (1999) 151–204. [CrossRef] [Google Scholar]
- Yarin A.L., Brenn G., Kastner O., Tropea C., Drying of acoustically levitated droplets of liquid-solid suspensions: evaporation and crust formation, Phys. Fluid. 14 (2002) 2289–2298. [CrossRef] [Google Scholar]
- Yarin A.L., Brenn G., Rensink D., Evaporation of acoustically levitated droplets of binary liquid mixtures, Int. J. Heat Fluid Flow. 23 (2002) 471–486. [CrossRef] [Google Scholar]
- Yarin A.L., Pfaffenlehner M., Tropea C., On the acoustic levitation of droplets, J. Fluid Mech. 356 (1998) 65–91. [CrossRef] [MathSciNet] [Google Scholar]
- Zbicinski I., Development and experimental verification of momentum, heat and mass transfer model in spray drying, Chem. Eng. J. 58 (1995) 123–133. [Google Scholar]
- Zbicinski I., Grabowski S., Strumillo C., Kiraly L., Krzanowski W., Mathematical modelling of spray drying, Comp. Chem. Eng. 12 (1988) 209–214. [CrossRef] [Google Scholar]
- Zbicinski I., Li X., Conditions for accurate CFD modeling of spray-drying process, Dry. Technol. 24 (2006) 1109–1114. [CrossRef] [Google Scholar]
- Zbicinski I., Strumillo C., Delag A., Drying kinetics and particle residence time in spray drying, Dry. Technol. 20 (2002) 1751–1768. [CrossRef] [Google Scholar]
- Zogzas N.P., Maroulis Z.B., Effective moisture diffusivity estimation from drying data. A comparison between various methods of analysis, Dry. Technol. 14 (1996) 1543–1573. [CrossRef] [Google Scholar]
Appendix I
CORRELATIONS USED IN THE CALCULATIONS


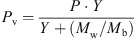

Vapor pressure at saturated conditions [67]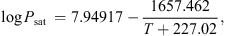 where T is expressed in °C and P
sat in Torr.
where T is expressed in °C and P
sat in Torr.
Specific heat of air-vapor mixture (J·kg−1·K−1) [39] where T is expressed in K and is suitable for 295 K < T < 800 K, R
2 = 0.9995.
where T is expressed in K and is suitable for 295 K < T < 800 K, R
2 = 0.9995.
Specific heat of water-vapor mixture (J·kg−1·K−1)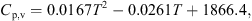 where T is expressed in °C.
where T is expressed in °C.
Viscosity of air (MPa·s) [39]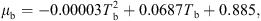 where T is expressed in K and suitable for 250 K < T
b < 400 K, R
2 = 0.9996.
where T is expressed in K and suitable for 250 K < T
b < 400 K, R
2 = 0.9996.
Density of air-vapor mixture (kg·m−3) [80]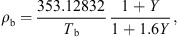 where T
b
is expressed in K.
where T
b
is expressed in K.
Diffusivity of air-vapor mixture (m2·s−1) [39]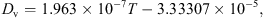 where T is expressed in K and suitable for 293 K < T < 373 K, R
2 = 1.0.
where T is expressed in K and suitable for 293 K < T < 373 K, R
2 = 1.0.
Thermal conductivity of air-vapor mixture (W·m−1·K−1) [39] where T is expressed in K.
where T is expressed in K.
Nomenclature
Letters
A C : cross-section area of atomizer pipe (channel) (m2)
b : thickness of liquid jet at the orifice (m)
C : GAB isotherm model parameter (–)
C 0 : GAB isotherm model constant (–)
C p : specific heat capacity (J·kg−1·K−1)
d p : diameter of droplet or particle (m)
D 3/2 : Sauter mean diameter (m)
D C : diameter of atomizer pipe (channel) (m)
D e : effective diameter of drying chamber (m)
D v : air-vapor diffusion coefficient (m2·s−1)
E isi : kinetic constant from solubility model (J·mol−1)
∆E v : apparent activation energy (J·mol−1)
∆E v,b : equilibrium activation energy (J·mol−1)
g : universal gravitational constant (= 9.8 m·s−2)
h : convective heat-transfer coefficient (W·m−2·K−1)
h m : mass-transfer coefficient (m·s−1)
∆H 1 : enthalpy parameter from GAB model (J·kg−1)
∆H 2 : enthalpy parameter from GAB model (J·kg−1)
∆H L : latent heat of vaporization (J·kg−1)
k : thermal conductivity (W·m−1·K−1)
K : GAB isotherm model parameter (–)
K 0 : GAB isotherm model constant (–)
k g : constant from the Gordon-Taylor model
k isi : kinetic constant from solubility model (mL·s−1)
l : axial distance in dryer (m)
m o : monolayer moisture content (kg·kg−1)
M : molecular weight (g·mol−1)
r isi : rate of insoluble material formation (mL·s−1)
R g : universal gas constant (= 8.314 J·mol−1·K−1)
T g : glass-transition temperature (K)
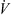 :
volumetric-flow rate (m3·s−1)
:
volumetric-flow rate (m3·s−1)
U : overall heat-transfer coefficient for heat loss (W·m−2·K−1)
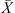 :
average droplet moisture content (dry basis) (kg·kg−1)
:
average droplet moisture content (dry basis) (kg·kg−1)
X 0 : initial moisture content (dry basis) (kg·kg−1)
X b : equilibrium moisture content (dry basis) (kg·kg−1)
Y : air absolute humidity (dry basis) (kg·kg−1)
Greek symbols
β : shrinkage model constant (–)
θ : number of droplets/particles (–)
Subscripts
All Tables
All Figures
 |
Figure 1. Relative activation energy profiles to be used in the REA for the drying of skim milk of 20, 30, 40, 50, 55 and 60 (all wt%, dry basis) initial solids contents. |
| In the text | |
 |
Figure 2. (a) Air temperature profiles predicted by the 1-D simulation tool and (b) outlet air temperatures from drying trials, 1-D simulation tool and SD2P® software. |
| In the text | |
 |
Figure 3. (a) Air humidity profiles predicted by the 1-D simulation tool and (b) outlet air humidity from drying trials, 1-D simulation tool and SD2P® software. |
| In the text | |
 |
Figure 4. (a) Powder moisture content profiles predicted by the 1-D simulation tool and (b) outlet powder moisture contents from drying trials, 1-D simulation tool and SD2P® software. |
| In the text | |
 |
Figure 5. Droplet and air velocity profiles predicted by the 1-D simulation tool. |
| In the text | |
 |
Figure 6. (a) Glass-transition temperature (T g) and product temperature profiles and (b) insolubility index profiles estimated by the 1-D simulation tool for the skim milk drying trials. |
| In the text | |