| Issue |
Dairy Sci. Technol.
Volume 90, Number 2-3, March–June 2010
Special Issue: Selected papers from 4th International Symposium on Spray Dried Dairy Products, 15-17th April 2009, Melbourne, Australia |
|
|---|---|---|
| Page(s) | 211 - 224 | |
| DOI | https://doi.org/10.1051/dst/2010015 | |
| Published online | 26 April 2010 | |
Review
An overview of the recent advances in spray-drying
喷雾干燥技术的研究进展—综述
Récentes avancées dans la conception et l’optimisation des installations de séchage par pulvérisation : une vue d’ensemble
1
National University of Singapore, Singapore
119260, Singapore
2
Institute of Chemical Industries of Forestry Products, Nanjing
210042, P. R. China
3
Department of Chemical Engineering, Monash University, Clayton, Victoria, Australia
* Corresponding author (通讯作者): dong.chen@eng.monash.edu.au
Received:
31
August
2009
Revised:
11
February
2010
Accepted:
11
February
2010
A global overview is presented of recent developments in spray drying. Recent advances in computational fluid dynamics modeling have provided new insights into the flow processes occurring within the spray chamber. This is important since detailed experimental measurements within an operating spray dryer are almost impossible due to the hostile environment of high-temperature two-phase flow, which may be unsteady, and the high cost that would have to incur. Some recent predictive studies on predicted effects of innovative chamber geometry, reduced pressure operation, operation in low dew-point air and superheated steam are presented. Also, a comparison is made between steady and unsteady state computations to highlight the critical issues. Predicted results on a horizontal spray chamber configuration are also presented. Finally, a brief survey is made on the recent literature on spray freeze-drying as well as multi-stage drying processes.
摘要
摘要 – 喷雾干燥技术的研究进展—综述。 本文对近年来喷雾干燥技术的研究进展进行了全面的概述。 近年来, 计算流体动力学模型为模拟喷雾室内流体流动过程提供了新的计算方法。由于干燥室内为高温下的两相流动体系, 因此这样环境下模拟和精确计算干燥过程的工作参数难度非常大。本文概述了采用预测模型的方法来预测干燥室的几何形状、减压操作、低雾化点下的操作以及过热蒸汽等因素对干燥工程的影响。 同样, 稳态和非稳态计算方法的对比也是近年来研究的热点问题。 作者还对水平喷雾干燥室构造的模拟和预测进行了论述。 最后对新兴的冷冻喷雾干燥和多级干燥的文献进行了简单的综述。
Résumé
Un inventaire des récents développements dans le domaine du séchage par pulvérisation est dressé. Les dernières avancées de la dynamique des fluides numérique ont permis d’obtenir de nouvelles représentations des processus d’écoulement ayant lieu à l’intérieur de la chambre de séchage. Ces modélisations sont très importantes car des mesures expérimentales détaillées à l’intérieur d’une installation de séchage en fonctionnement sont pratiquement impossibles à réaliser, en raison des conditions hostiles liées au flux à température élevée de deux phases, pouvant être irrégulier, et aux coûts qui seraient engendrés. Des études prédictives récentes sur les effets d’une géométrie innovante de la chambre, de conditions de pression réduite, d’air à bas point de rosée et de vapeur surchauffée, sont notamment présentées. Une comparaison des calculs réalisés dans des conditions stables ou instables est également réalisée afin de mettre en lumière les points critiques. Les résultats de la prédiction pour une configuration de chambre horizontale sont présentés. Enfin, les dernières publications sur le couplage séchage par pulvérisation-lyophilisation et les procédés de séchage multi-étage sont présentées rapidement.
Key words: computational fluid dynamics / modeling / spray drying / CFD
关键字 : 计算流体动力学 / 模拟 / 喷雾干燥 / CFD
Mots clés : dynamique des fluides / modélisation / séchage par pulvérisation / CFD
© INRA, EDP Sciences, 2010
1. INTRODUCTION
Because milk powder has many advantages, e.g., long shelf-life due to low moisture content in the powder, low packing and transport costs and facilitation of product utilization, it plays a significant role among dairy products. For example, in France, in 2000, the consumption of milk powder was almost the same as that of fresh skim milk. Spray drying converts liquid form into an engineered powder product in one step. Such drying technology is also suitable to dry many heat-sensitive products, e.g., dairy products, foods and pharmaceuticals, due to the short drying time and ability to obtain a powder form product [8].
There are three main types of atomizers to convert a feed liquid stream into a spray of droplets, i.e., pressure nozzle, two-fluid nozzle and centrifugal wheel atomizer [18]. The selection of the atomization method is dependent on the product requirements as well as initial feed physical properties. Recently, ultrasonic and electrostatic nozzles have been reported to be used as atomizers in small-scale spray drying operations. They can produce a narrow size distribution of droplets for production of a mono-disperse product. For the contact of the drying medium and the atomized droplets, there are three possible types of gas-droplet contact, i.e., counter-current, co-current and mixed flow. In co-current contact, the droplets passing through the drying chamber move in the same direction as the drying medium. In a counter-current operation, they flow in opposite directions and hence semi-dried or dried particles may be exposed to the drying medium at a higher temperature. This can damage thermo-sensitive powders, such as milk products. Therefore, the majority of dairy products are dried in concurrent spray dryers [45].
Spray drying chambers are mainly of the vertical type [3]. Vertical vessels with a cylindrical cross-section and a conical bottom are used most frequently [36]. The size of the cylindrical and conical sections depends on the application. Huang et al. [22, 24] have tested a horizontal spray dryer (HSD) as well as a two-stage horizontal dryer using the computational fluid dynamic (CFD) method. A few commercial operations do use a horizontal layout but it is still not popular and its performance characteristics are not well understood yet.
O’Callaghan and Cunningham [42] have pointed out the need for the use of modern process control techniques in large-scale spray dryers and the use of “white box” models as opposed to the more traditional “black box” models. There is trend toward Model Predictive Control (MPC) which requires ability to forecast system behavior or response to upsets. Currently in milk production, empirical or semi-empirical models based on past experience are used for control purposes. Since the process involved is highly nonlinear, it has the potential to lead to large uncertainties and thus production of off-spec products, which can be very costly for large-scale plants. A “white box” model based on the fundamental equations of conservation can be used to assist in MPC, as discussed by Verdurmen et al. [58]. As noted elsewhere the major deterrent to such modeling is the difficulty in detailed validation of CFD models due to the impossibility of obtaining local data within an operating spray dryer even at a pilot scale. Most authors “validate” their CFD results using only outlet data in an averaged manner. This does not represent true validation since compensating errors within the chamber computations can yield a good match at the outlet of the chamber. In principle, it is possible to model the effects of stickiness, agglomeration, etc., using CFD models but such models do depend necessarily on a lot of empirical input and hence much uncertainty.
Although spray drying is used in many industries, fundamental understanding is still lacking. For example, the design of spray drying is probably still dependent on the designer’s experience and/or extensive pilot-scale testing. Even so, droplet/particle deposition on the chamber walls is highly undesirable problem. In this paper, an overview is presented of the recent developments in spray drying technology including the fundamentals and applications of spray drying in the dairy processing as well as the recent advances in modeling spray drying using CFDs.
2. THE DEVELOPMENTS IN SPRAY DRYING PROCESS USED IN DAIRY INDUSTRY
An industrial milk powder production plant is a typical example of spray drying plant in the food industry. After cooling, pasteurization and homogenization stages, the milk emulsion to be dried is concentrated up to 48–52 wt% of total solids in a multiple-effect evaporator system (typically of the falling-film type or plate type) [46]. Then, this concentrated emulsion is ready for spray drying. A one-stage spray dryer is used in some plants. The concentrated emulsion is atomized into droplets of 1–200 μm by a centrifugal wheel atomizer or a high pressure spray nozzle, located at the top of the spray chamber. The droplets fall into the spray chamber in a concurrent flow with a hot filtered air; the moisture in the emulsion droplets is removed by hot air. Milk droplets shrink in size as water is evaporated from its surface. Finally, the droplets lose most of their moisture and become particles with a solid crust formed at their surface. In the single-stage spray drying process, a pneumatic conveying system is always needed to remove the final fraction of moisture from the nominally dried powder and to cool it prior to storage. In the single-stage spray drying system, energy consumption is high. The fine powder product is not readily dissolved in water. For these reasons, a multi-stage drying system was devised in the 1970s. In this system, a vibro-fluidized bed drying (VFBD) and cooling system follows below the spray drying chamber. The VFBD consists of a rectangular chamber and an inclined or wrinkled perforated plate inside it. Hot air at 80–120 °C is first used to reduce the particle moisture from 8–9 wt% to 3–4 wt%, as the particles move along the perforated plate. Downstream of the VFBD, cooling with dehumidified air is always used to cool the dried particle before safe packaging (Xiao Dong Chen, Industrial experiences, 1991–1999).
In the 1980s, a three-stage drying system was developed for milk drying [54] to enhance the overall performance to a higher level as the production capacity requirements increased. In this system, a conventional fluidized bed is inserted into the conical bottom of the spray drying chamber. Hot air at 90–100 °C is used to fluidize the semi-dried milk powder. A VFBD then follows downstream. Drying and cooling operations can be better controlled in the second and third stages. The fine powders from the spray drying chamber and VFBD are recycled into the spray drying chamber. Thus, agglomerated powders are finally obtained. Recycling the fine particles that have been classified out of the fluidized bed(s) and/or cyclone(s) may be done at different locations in the primary chamber of spray dryer for agglomeration purpose. The Niro method is called “straight-through method” that returns the fines and feeds them into the liquid atomization zone to induce agglomeration [4, 61]. This enhances powder quality by control of the particle size distribution and reduced dustiness. It is reported that a three-stage drying process can save 20% of energy consumption compared to the single-stage spray drying system [23, 60]. A Chinese company, Linzhou China Ltd. (www.linzhou.com), has used such a process also to dry coconut juice.
As discussed earlier, the multi-stage drying process is preferred in dairy product processing due to energy efficiency and agglomeration of the particles obtained which makes the product instantly soluble in water. Some variations of this technique can be found in the food industry. The Linzhou China Ltd. used the two-stage spray drying process to obtain the powder of fat. The difference from the other process is that the drying air is exhausted from the middle of the drying chamber. The cyclones can be omitted if a suitable bag filter is installed in the middle of the chamber. Another variation consists of a conveying belt drying system that is installed at the bottom of spray drying chamber (Niro Denmark Ltd., www.niro.com). The partially wet particles can be continuously dried on the belt in a lower temperature environment. Such a combined drying system is suitable for heat-sensitive products, such as dairy foods. Multi-staging reduces the size of the spray drying chamber considerably.
Pulse combustion spray drying has been reported as a relatively new but not-yet-popular development of spray drying. It can be used to dry milk. Thompson [55] compared the recovered milk by three drying methods, i.e., roller dryer, spray dryer and pulse combustion dryer. They found that the pulse combustion dryer produced the least residual moisture in the final product followed by the roller dryer. The milk product from pulse combustion drying had the best solubility compared to that by regular spray dryer and roller dryer. Wu and Liu [65] used the CFD method to model such a process. They found that the drying rates are much faster than in normal spray drying. Xiao et al. [66] have investigated the effects of atomizing parameters on droplet characteristics in a pulse combustion spray dryer.
Generally, air is used as the drying medium for spray drying. Recently, Ducept et al. [7] and Frydman et al. [9] used a commercial code to simulate a spray dryer using superheated steam as the drying medium. However, in their models, the elevation of the boiling point for suspension was not considered. Although superheated steam can provide a number of advantages, e.g., excellent energy efficiency if the exhaust steam can be utilized elsewhere in the plant and also advantages resulting from the absence of oxygen, the equipment and operation are more costly and complex. Pilot tests are being conducted commercially to examine the product quality of steam-dried milk powders.
Freeze-drying is a good way to obtain high-quality heat-sensitive products. Sonner [49] used liquid nitrogen to obtain frozen powder. The frozen powder is transferred to a vacuum freeze-drying chamber. They found that the drying time is reduced significantly compared to normal freeze-drying. More recently, Leuenberger et al. [35] reported spray freeze-drying of pharmaceuticals using cooled and dehumidified air obtained by dry ice. Rogers et al. [47] investigated milk powder characteristics in laboratory-scale spray freeze-dryer using liquid nitrogen as the cryogen. However, such a process is still not mature and needs to be developed on the industrial scale [21]. In their process, they used the cooled and dehumidified air instead of liquid nitrogen or dry ice. Their experimental results showed that the process time for atmospheric freeze-drying of milk needed 9–10 h. More voids in the dried milk powder were seen under a microscope, when compared with the conventional spray dried milk powder. It is unlikely that spray freeze-drying will become a viable process for drying of milk in large scale, however. With the increase in production of highly valuable protein components extracted from milk, which are in much less quantities but highly bioactive, spray freeze-drying may become manufacture tool.
3. MATHEMATICAL MODELING OF SPRAY DRYERS
Although spray drying systems are widely used in diverse industries, their design is still based on empirical methods and experience. Systematic studies must be carried out on spray formation and air flow, as well as heat and mass transfer in spray-air contact for optimizing and controlling the drying mechanisms, to achieve the highest quality of powders produced. This process-product association requires a complex model, which must predict not only the material drying kinetics as a function of the spray drying (SD) operation variables, but also changes in powder properties during drying. Such combination can be established by introducing into the SD model empirical correlations for predicting the most important product quality requirements (statistical approach) or by describing mechanisms of change of the material properties during drying (kinetic approach).
Since 1970s, many attempts have been made at modeling spray drying. An important advancement was made by Parti and Palancz [44]. They formulated a mathematical description that included conservation of momentum, heat and mass between the continuous and discrete phases. But their solutions were inadequate near the atomizer. Later, Katta and Gauvin [28] created a model of spray drying which divided the chamber into a jet region and an annular free entrainment region. The boundary conditions between these two regions were set from empirical data. They assumed that the gas flow was not affected by the presence of the droplets or particles. Validation was done using data on water sprays.
Crowe et al. [6] first proposed an axi-symmetric spray drying model called the particle-source-in-cell model (PSI-Cell model). This model included two-way mass, momentum and thermal coupling. They developed a method to solve the Navier-Stokes equations and continuity equation where the droplets were treated as sources of mass, momentum and energy to the gaseous phase. In this model, the gas phase was regarded as a continuum (Eulerian approach) and is described by pressure, velocity, and temperature and humidity fields. The droplets or particles were treated as a discrete phase, which was characterized by velocity, temperature, composition and the size along trajectories (Lagrangian approach). It incorporated a finite difference scheme for both the continuum and discrete phases.
In 1987, a spray dryer with a 0.76-m diameter chamber having a 1.44 m height was modeled using a commercial CFD (FLOW3D) program [10, 43]. In this model, the PSI-Cell model was also implemented. The trajectories of typical small, medium and large droplets of water in drying chamber were computed. Kieviet [29] carried out measurements of airflow patterns and temperature profiles in a co-current pilot spray dryer (diameter 2.2 m). A CFD package (FLOW3D) was used for simulation. Good agreement was obtained by comparing the model results with measurements, although a two-dimensional axi-symmetric model was used for simulation.
Langrish and Zbicinski [34] used a CFD program to explore the effects of several parameters, e.g., adjusting the inlet geometry and reducing the spray angle, for decreasing wall deposits. Southwell and Langrish [50] also carried out the CFD simulations of typical spray dryers with co-current and counter-current flow using a commercial code (CFX). Reasonable comparison with the limit experimental data was made.
Straatsma et al. [51] developed a drying model that could describe the relation between the processing conditions of the drying process, energy consumption and the properties of the powder produced for a two-stage dryer. In their model, they assumed a near-equilibrium state of water vapor pressure between the powder and the outlet air, which eliminated the need for a detailed description of the heat and mass transfer phenomena during the drying process. However, this drying model could not predict the details inside the drying chamber. Straatsma et al. [52, 53] developed a new drying model DrySim that made use of CFD techniques to calculate the flow pattern, particle behavior, etc. Verdurmen et al. [58] used the DrySim program for modeling some industrial cases. However, this model is a two-dimensional model.
An industrial-scale spray dryer with a 7-m diameter chamber having a cylindrical height of 14 m with two pressure nozzles was modeled using CFD [21]. Good agreement was obtained between the model data and the plant. From the simulation results, they found that the upper cone connected with the inlet cylindrical pipe can reduce size of the recirculation zone, which is found in most spray dryers [20, 29]. In a spray dryer, agglomeration cannot be avoided. It always takes place within the droplet zone produced by an atomizer, between the droplets and semi-dried particles. In order to increase the solubility of the dried powder, e.g., skim milk, a fine return system is always installed in a spray dryer for skim milk since an agglomerated product is needed. It is known that agglomeration is quite difficult to control in a spray dryer. Main reason for this is the complex interaction of the process variables, e.g., atomization, contact between the atomization zone and the drying medium, and drying kinetics of the droplets and particles. Verdurmen et al. [57] carried out the well-known EDECAD project designed to develop an industrial computation model for predicting agglomerations in a spray dryer using CFD. In order to validate droplet collision and coalescence models, the experiments on spray interaction were carried out [41, 57]. Stochastic and direct simulation Monte Carlo collision and coalescence models approaches were implemented in the CFD codes they developed [2, 48, 57]. The “Design” tools developed by EDECAD project were validated in a pilot spray dryer [59]. This probably is the most comprehensive modeling study of spray dryers including many complex interactions.
All these models are a significant advance in modeling of spray drying because the mass, momentum and energy equations were solved with no restrictive assumptions about the drying chamber geometry and gas inlet conditions. These advantages allow one to investigate the new designs of drying chamber and the effects of inlet geometry variations on dryer performance. For example, Huang et al. [17] investigated several new chamber designs by CFD modeling approach, i.e., conical, lantern and hour-glass chamber geometries, for spray drying. They found that pure cone and lantern shapes can be used as viable drying chamber designs, although they are not yet used in industry. Pilot testing may be desirable for such novel chamber geometries. More work is needed along with the effect of supplemental inlet gas streams to see their potential benefits. One-stage and two-stage HSDs were investigated using CFD approach as well [19, 20]. The velocity magnitude contours are shown in Figure 1. It can be seen that there are some high velocity regions near each fluidized bed plate inlet. This blocks the droplets that might deposit at the bottom of the chamber in one-stage HSD. Also, the fluidized bed at the bottom of the chamber affects the chamber flow pattern as well, i.e., the high velocity region at the main inlet is extended. In a real drying condition, this may enhance heat and mass transfer between the droplets and drying medium.
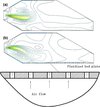 |
Figure 1. Velocity magnitude contours for one-stage and two-stage HSDs: (a) one-stage HSD and (b) two-stage HSD (the fluidized bed covers the entire bottom boundary of this device simulated). |
Xu et al. [67] have recently examined parabolic-shaped chamber geometries for hydro-cyclones, which also involve vortex flows similar to those in the conical section of a spray dryer. They reported significantly reduced erosion rates for such geometry. In spray drying, this may mean reduced wall deposits. It is an interesting but as-yet untested design.
Methods for reducing deposition in spray dryers can be classified into two types: those involved in reducing particle-wall contact and those that reduce the stickiness of particle-wall contact. Some recent work on the latter aspect involves manipulating the wall surface energy. This idea was proposed in a review by Bhandari and Howes [1] in which lower wall surface energy was found to result in less stickiness of the amorphous particle-wall contact. Although such an effect was not observed in a particle gun experiment [40], recent investigations on pilot-scale dryers revealed the potential of using wall material with lower surface energy [64] and other non-sticky wall material [30] to combat the deposition problem. The reduction mechanism was further confirmed with elevated wall temperatures, to mimic industrial operation, that lower surface energy reduces deposition of amorphous particles [63]. In the latter report, within a limited operational window, lower surface energy also improved the ease in removing the deposited particles. From some preliminary results, it was speculated that this might reduce the cleaning effort required for a spray dryer [63].
In terms of modeling of wall deposits using the CFD Lagrangian-Eulerian approach, mixed results on the modeling of deposition can be found in the literature [16, 18, 31]. Of course, one should not attribute this solely to the deposition model, as the airflow prediction also plays an important part in the accuracy of the models. Most CFD work utilizes the stick-upon-contact approach [18]. However, a particle may exhibit different degree of stickiness and impacting velocity or angle, depending on its location or moisture content. These will further affect the rebound characteristics of a particle. A first step in addressing the former aspect was proposed by Harvie et al. [16] in utilizing the sticky point, which is related to the glass transition and is a function of particle moisture and temperature, as a deposition criterion. While taking into account the particle stickiness, this approach does not consider the effect of impacting velocity and angle. Although the effect of these collision parameters is yet to be quantified in a spray dryer, it is known that particle restitution is sensitive to these parameters and will be interesting to incorporate these in future development of deposition models.
Huang and Mujumdar [19] investigated a spray dryer fitted with a centrifugal atomizer using CFD model. In their model, they modeled the rotary disk atomization into the disk side point injection which was the same as the holes in the disk. The path-lines from the air inlet of drying chamber are shown in Figure 2. It was seen that there was strong swirling just below the atomizer disk due to the disk rotation. This swirling significantly affected the flow pattern in the chamber. This was proved from the non-uniform temperature contours at planes X-Z and Y-Z, shown in Figure 3. It was also seen that there was a low-temperature region away from the central line at plane X-Z. It indicated that more droplets passed through this region due to the central swirling.
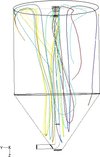 |
Figure 2. Path-lines from the air inlet of drying chamber. |
 |
Figure 3. Temperature contours at cut-planes X-Z and Y-Z. |
However, the works above all assumed steady flow in spray drying. A recent review suggests that the airflow pattern, specifically the central jet, has tendency to exhibit self-sustained oscillatory behavior and this is important to be accounted for in a CFD model. There are significant differences between the wall deposit rates and locations for steady and unsteady swirling flows. Of course, experimental verification is yet to be reported. While data on pilot size spray dryers are more realistically obtained for model validation, significant uncertainty still remains when the model is to be applied to full-scale dryers.
Initial work on the transient behavior involved visualization and measurement of the flow fluctuation in pilot-scale units [32, 50]. Langrish et al. [32] reported that there were low-frequency oscillations found in the flow field inside a 1.5-m diameter spray drying chamber during the measurements using a hot-wire anemometer. It was seen that the flow in the drying chamber is not stable. So the steady flow model might not predict well the performance of the spray drying in some applications. The time-dependent model is necessary for accurate modeling of spray drying. Oakley and Bahu [43] used the CFDS-FLOW3D™ program to run in time-dependent mode of spray drying. They found that there were low-frequency oscillations when the significant swirl in the gas inlet is sufficient. Guo et al. [11] carried out a fully three-dimensional and transient simulation using CFX4™. The simulated results showed that there were both swinging and swirling oscillations of a regular period, even with no inlet swirling.
In order to discern these transient flow mechanisms, it was later proposed that flow in a typical SD geometry is similar to that of a confined jet under sudden expansion. This was followed by a series of papers on numerical studies of such small-scale sudden pipe expansion systems which provided further evidence to the self-sustained oscillation for such geometry which is similar to the SD [12–14]. Along this line, the effect of inlet swirls on such self-sustained oscillation was studied. Usage of inlet swirls, a common industrial design, was shown to aggravate the transient behavior [33].
These recent findings seem to delineate the obsolete of the steady state approach. However, transient simulation would imply much higher simulation time and resources due to: (1) small time step required for such systems and (2) 3D domain required as 2D or axi-symmetric model is not sufficient to capture the jet precession and flapping motion. Furthermore, from our modeling experience, a transient simulation introduces additional uncertainty in choosing the time step and spatial resolution required in capturing these transient vortices. In the study of the sudden pipe or cavity expansion systems, self-sustained oscillation was found to be geometry aspect ratio and inlet condition dependent [12, 15, 37]. In view of the reasonable prediction via the steady state approach in some of the earlier work mentioned above, this suggests that there may be certain operating and geometry combinations in which the steady state will prove to be a good approximation. Kota and Langrish [30], in their numerical study, noted that the mild transient jet movement of a non-swirling inlet flow only caused small fluctuations in the overall particle deposition trend at different transient simulation time.
Therefore, it will be interesting and practical to determine the possibility of such boundaries or “map” to discern the suitability of the steady state or transient approach in actual dryer geometries for effective application of the CFD tool. As would be noted, most of the studies on the transient behavior were mainly focused on the non-swirling and inlet swirling flows, without much attention being placed on the atomizer-induced swirling flows. Some preliminary work is currently underway in these two areas mentioned. Apart from that, Langrish et al. [33] also noted that airflow studies undertaken hitherto are mainly without inclusion of the droplets or particles. It is unclear how the droplet-air momentum transfer near the inlet region will affect the possible transient behavior of the jet. Further work was suggested in this area [33].
More recently, an unsteady model in a spray dryer fitted with a rotary disk was studied by Woo [62]. Two cases, i.e., Case A (0.8-m diameter drying chamber) and Case A with smaller radius and higher flow rate at the inlet, were investigated. Non-periodic and unstable fluctuation patterns were observed. These illustrate the dependence of the jet in an actual spray dryer on the radial expansion ratio and inlet Reynolds number which quantified the feedback effect when the jet encountered any obstruction in the confined geometry or due to the backflow hydrodynamics. In this case, it was the constriction at the outlet and the recirculation region at the outer annular region of the chamber. On the effect of Reynolds number, Maurel et al. [37] have shown, with their small-scale laboratory experiments, that the oscillation regimes of non-swirling confined jets under sudden expansion are sensitive to this parameter. These findings also explained why few workers reported semi-symmetric and quasi-steady state solution in chambers of larger diameter for non-rotating flows [56].
In Figure 4, axial velocity contours at different time intervals for the two tested cases are shown. The contour plots at different flow times for Case A are shown in Figure 4a. Contrary to the findings of Guo et al. [15] on different dryer geometries, it was found that there was no significant unsteadiness in the simulation without atomizer rotation. It can be seen from Figure 4b that the tip of the jet stretched and expanded. This occurred in many directions in an unsteady manner, similar to the findings of Guo et al. [15].
 |
Figure 4. Axial velocity contours at different time intervals for (a) Case A and (b) Case A with smaller radius and higher flow rate (plan view is taken at 0.9 m from the ceiling). |
However, lack of carefully obtained experimental data – primarily due to often the proprietary nature of the process and difficulty of making the necessary detailed measurements – is currently hampering the development of CFD-based design and analysis of spray dryers. It is quite possible that the numerical predictions almost as reliable as experimental data can be obtained within the spray dryer chamber under operating conditions. Mezhericher et al. [38, 39] explored droplet interactions in a pilot-scale dryer numerically and further examined the effects of 2D or 3D modeling approaches. Most recently, Jin and Chen [25–27] have conducted transient CFD modeling of large-scale industrial spray drying processes including an investigation on powder deposition in a large-scale dryer [26] that has 9 tonnes powder production per hour [5]. There are still some limitations to depending entirely on the CFD approach since it does not typically include reliable models based on experience for quality changes, attrition or agglomeration of particles that can occur within the chamber.
4. CONCLUSION
Spray drying is an important step in dairy powder processing. Of course, it is a technology that has a very wide range of applications and in this review greater attention has been paid to those applied in the dairy industry. Dried dairy products have long shelf-life and are easy to be used at remote locations from the production area or country hence having a great influence on international trade. Three-stage drying system is commonly used, which includes primary drying (spray drying) and fluidized bed drying (second and third stages). This system is by far the most efficient approach. Recently, some new drying technologies, e.g., spray freeze-drying and superheated steam spray drying, are also developed. These new drying technologies are still exploratory and due to the potentially higher costs, they are considered for some special products that are heat-sensitive and pricy.
It is noteworthy that with CFD technology developing rapidly, mathematical modeling has become a useful tool to simulate the complex drying process and guide future developments without excessive experimental trial-and-error associated costs. However, measurements at an industrial scale to validate the computer models are hard to come by. There are few experimental data at a large industrial scale (such as several T of powder produced per hour). This does hamper the industrial confidence upon the use of CFD software. Efforts are being placed to fill such a gap in both academia and industry, in particular, those who do work together coherently.
References
- Bhandari B., Howes T., Relating the stickiness property of foods undergoing drying and dried products to their surface energetic, Drying Technol. 23 (2005) 791–797. [Google Scholar]
- Blei S., Sommerfeld M., Computation of agglomeration for non-uniform dispersed phase properties – an extended stochastic collision model, in: Proceedings of the 5th International Conference on Multiphase Flow, 30 May–4 June 2004, ICMF’04, Yokohama, Japan. [Google Scholar]
- Caric M., Concentrated and Dried Dairy Products, VCH Publishers, New York, USA, 1994. [Google Scholar]
- Chen X.D., Whole milk powder agglomeration – principle and practice, in: Chen X.D. (Ed.), Milk Powders for the Future, Dunmore Press, Palmerston North, New Zealand, 1992. [Google Scholar]
- Chen X.D., Lake R., Jebson S., Study of milk powder deposition on a large industrial dryer, Trans. IChemE: Bio-Process. Food Process. 71 (1993) 180–186. [Google Scholar]
- Crowe C.T., Sharma M.P., Stock D.E., The particle-source-in-cell (PSI-Cell) model for gas-droplet flows, J. Fluid Eng. 9 (1977) 325–332. [Google Scholar]
- Ducept F., Sionneau M., Vasseur J., Superheated steam dryer: simulations and experiments on product drying, Chem. Eng. J. 86 (2002) 75–83. [CrossRef] [Google Scholar]
- Filkova I., Huang L.X., Mujumdar A.S., Industrial spray drying systems, in: Mujumdar A.S.(Ed.), Handbook of Industrial Drying, Taylor & Francis, New York, USA, 2007, pp. 215–257. [Google Scholar]
- Frydman A., Vasseur J., Ducept F., Moureh J., Simulation of spray drying in superheated steam using computational fluid dynamics, Drying Technol. 17 (1999) 1313–1326. [CrossRef] [Google Scholar]
- Goldberg J.E., Prediction of Spray Dryer Performance, Ph.D. Thesis, University of Oxford, UK, 1987. [Google Scholar]
- Guo B., Langrish T.A.G., Fletcher D.F., Time-dependent simulation of turbulent flows in axisymmetric sudden expansions, in: Thompson M.C., Hourigan K.(Eds.), Proceedings 13th Australasian Fluid Mechanics Conference, Melbourne, Australia, 1998, pp. 283–286. [Google Scholar]
- Guo B., Langrish T.A.G., Fletcher D.F., Numerical simulation of unsteady turbulent flow in axisymmetric sudden expansions, J. Fluids Eng. 123 (2001) 574–587. [CrossRef] [Google Scholar]
- Guo B., Langrish T.A.G., Fletcher D.F., Simulation of turbulent swirl flow in an axisymetric sudden expansion, AIAA J. 39 (2001) 96–102. [CrossRef] [Google Scholar]
- Guo B., Langrish T.A.G., Fletcher D.F., CFD simulation of precession in sudden pipe expansion flows with low inlet swirl, Appl. Math. Model. 26 (2002) 1–15. [CrossRef] [Google Scholar]
- Guo B., Langrish T.A.G., Fletcher D.F., Simulation of gas flow instability in a spray dryer, Chem. Eng. Res. Des. 81 (2003) 631–638. [CrossRef] [Google Scholar]
- Harvie D.J.E., Langrish T.A.G., Fletcher D.F., A computational fluid dynamics study of a tall-form spray dryer, Trans. IChemE 80 (2002) 163–175. [Google Scholar]
- Huang L.X., Kumar K., Mujumdar A.S., Use of computational fluid dynamics to evaluate alternative spray dryer chamber configurations, Drying Technol. 21 (2003) 385–412. [CrossRef] [Google Scholar]
- Huang L.X., Mujumdar A.S., Spray drying: principle and practice, in: Mujumdar A.S.(Ed.)Guide to Industrial Drying, 2nd enhanced edn., Colour Publications Pvt. Ltd., Mumbai, India, 2004, pp. 143–169. [Google Scholar]
- Huang L.X., Mujumdar A.S., Development of a new innovative conceptual design for horizontal spray dryer via mathematical modeling, Drying Technol. 23 (2005) 1169–1187. [CrossRef] [Google Scholar]
- Huang L.X., Mujumdar A.S., Numerical study of two-stage horizontal spray dryers using computational fluid dynamics, Drying Technol. 24 (2006) 727–733. [CrossRef] [Google Scholar]
- Huang L.X., Mujumdar A.S., Simulation of an industrial spray dryer and prediction of off-design performance, Drying Technol. 25 (2007) 703–714. [CrossRef] [Google Scholar]
- Huang L.X., Passos M.L., Kumar K., Mujumdar A.S., A three-dimensional simulation of a spray dryer fitted with a rotary atomizer, Drying Technol. 23 (2005) 1859–1873. [CrossRef] [Google Scholar]
- Huang L.X., Wang Z., Tang J., Recent progress of spray drying in China [in Chinese], Chem. Eng. (China) 29 (2001) 51–55. [Google Scholar]
- Huang L.X., Zheng W.H., Wang C.Z., Mujumdar A.S., Leuenberger H., Spray freeze drying and its applications in drying of plant extracts and pharmaceuticals [in Chinese], Chem. Ind. For. Prod. 27 (2007) 143–146. [Google Scholar]
- Jin Y., Chen X.D., A three-dimensional numerical study of the gas/particle interactions in an industrial-scale spray dryer for milk powder production, Drying Technol. 27 (2009) 1018–1027. [CrossRef] [Google Scholar]
- Jin Y., Chen X.D., Numerical study of the drying process of different sized particles in an industrial-scale spray dryer, Drying Technol. 27 (2009) 371–381. [CrossRef] [Google Scholar]
- Jin Y., Chen X.D., A numerical model for the particle deposition on industrial milk dryers, Drying Technol. (to appear). [Google Scholar]
- Katta S., Gauvin W.H., Some fundamental aspects of spray drying, AIChE J. 21 (1975) 143–150. [CrossRef] [Google Scholar]
- Kieviet F.G., Modelling Quality in Spray Drying, Ph.D. Thesis, Endinhoven University of Technology, The Netherlands, 1997. [Google Scholar]
- Kota K., Langrish T.A.G., Fluxes and patterns of wall deposits for skim milk in a pilot-scale spray dryer, Drying Technol. 24 (2006) 993–1001. [CrossRef] [Google Scholar]
- Kota K., Langrish T.A.G., Prediction of deposition patterns in a pilot-scale spray dryer using computational fluid dynamics (CFD) simulations, Chem. Prod. Process Model. 2 (2007) Article 26. [Google Scholar]
- Langrish T.A.G., Oakley D.E., Keey R.B., Bahu R.E., Hutchinson C.A., Time-dependent flow patterns in spray dryers, Trans. IChemE 71 (1993) 355–360. [Google Scholar]
- Langrish T.A.G., Williams J., Fletcher D.F., Simulation of the effects of inlet swirl on gas flow patterns in a pilot-scale spray dryer, Chem. Eng. Res. Des. 82 (2004) 821–833. [CrossRef] [Google Scholar]
- Langrish T.A.G., Zbicinski I., The effects of air inlet geometry and spray angle on the wall deposition rate in spray dryers, Trans. IChemE 72 (1994) 420–430. [Google Scholar]
- Leuenberger H., Plitzko M., Puchkov M., Spray freeze drying in a fluidized bed at normal and low pressure, Drying Technol. 24 (2006) 711–719. [CrossRef] [Google Scholar]
- Masters K., Spray Drying Handbook, 5th edn., John Wiley & Sons Inc., New York, USA, 1991, pp. 725–726. [Google Scholar]
- Maurel A., Ern P., Zielinska B.J.A., Wesfreid J.E., Experimental study of self-sustained oscillations in a confined jet, Phys. Rev. E 54 (1996) 3643–3651. [Google Scholar]
- Mezhericher M., Levy A., Borde I., Droplet-droplet interactions in spray drying by using 2D Computational Fluid Dynamics, Drying Technol. 26 (2008) 265–282. [CrossRef] [Google Scholar]
- Mezhericher M., Levy A., Borde I., Modeling of droplet drying in spray chambers using 2D and 3D computational fluid dynamics, Drying Technol. 27 (2009) 359–370. [CrossRef] [Google Scholar]
- Murthi R.A., Paterson A.H.J., Pearce D., Bronlund J.E., Controlling SMP stickiness by changing the wall material: feasible or not?, in: Proceedings of Chemeca, Auckland, New Zealand, 2006, CD-ROM, paper 209. [Google Scholar]
- Nhumaio G.C.S., Watkins A.P., Yule A.J., Experiments and CFD predictions of two overlapping water sprays issued from air-assist atomizers, in: Proceedings ILASS Europe 19th Annual Conference on Liquid Atomization and Spray Systems, 6–8 September 2004, Nottingham, UK, 2004. [Google Scholar]
- O’Callaghan J., Cunningham P., Modern process control techniques in the production of dried milk – a review, Lait 85 (2005) 335–342. [CrossRef] [EDP Sciences] [Google Scholar]
- Oakley D.E., Bahu R.E., Spray/gas mixing behavior within spray dryers, in: Mujumdar A.S., Filkova I.(Eds.), Drying’91, Elsevier, Amsterdam, The Netherlands, 1991. [Google Scholar]
- Parti M., Palancz B., Mathematical model for spray drying, Chem. Eng. Sci. 29 (1974) 355–362. [CrossRef] [Google Scholar]
- Passos M.L., Mujumdar A.S., Mathematical models for improving spray drying processes for foods, Stewart Post-harvest Review, www.stewartpostharvest.com, 2005. [Google Scholar]
- Pisecky J., Evaporation and spray drying in the dairy industry, in: Mujumdar A.S. (Ed.), Handbook of Industrial Drying, Vol. 1, 2nd edn., Marcel Dekker Inc., New York, USA, 1995, pp. 715–742. [Google Scholar]
- Rogers S., Wu D., Saunders J., Chen X.D., Characteristics of milk powders produced by spray freeze drying, Drying Technol. 26 (2008) 404–412. [Google Scholar]
- Sommerfeld M., Validation of a stochastic Lagrangian modeling approach for inter-particle collisions in homogeneous isotropic turbulence, Int. J. Multiphase Flow 27 (2001) 1829–1858. [CrossRef] [Google Scholar]
- Sonner C., Protein-Loaded Powders by Spray Freeze Drying, Ph.D. Thesis, Department of Pharmaceutics, Friedrich-Alexandar University, Erlangen, Germany, 2002. [Google Scholar]
- Southwell D.B., Langrish T.A.G., Observations of flow patterns in a spray dryer, Drying Technol. 18 (2000) 661–685. [CrossRef] [Google Scholar]
- Straatsma J., van Houwelingen G., Meulman A.P., Steenbergen A.E., DrySPEC2: a computer model of a two-stage dryer, J. Soc. Dairy Technol. 44 (1991) 107–111. [CrossRef] [Google Scholar]
- Straatsma J., van Houwelingen G., Steenbergen A.E., De Jong P., Spray drying of food products: 1. Simulation model, J. Food Eng. 42 (1999) 67–72. [CrossRef] [Google Scholar]
- Straatsma J., van Houwelingen G., Steenbergen A.E., De Jong P., Spray drying of food products: 2. Prediction of insolubility, J. Food Eng. 42 (1999) 73–77. [CrossRef] [Google Scholar]
- Tang J.X., Huang L.X., Wang Z.L., Three-stage drying system and its application in dairy product processing [in Chinese], J. Nanjing Forestry 21 (1997) 56–58. [Google Scholar]
- Thompson R.I., Nutrient Profile, Functional Properties and Microstructure of Dried Waste Milk Product for Use as a Potential Animal Feed, Ph.D. Thesis, Louisiana State University, USA, 2002. [Google Scholar]
- Ullum T., Simulation of a spray dryer with rotary atomizer: the appearance of vortex breakdown, in: Proceedings of the 15th International Drying Symposium, 20–23 August 2006, Budapest, Hungary, pp. 251–257. [Google Scholar]
- Verdurmen R.E.M., Menn P., Ritzert J., Blei S., Nhumaio G.C.S., Sonne Sørensen T., Gunsing M., Straatsma J., Verschueren M., Sibeijn M., Schulte G., Fritsching U., Bauckhage K., Tropea C., Sommerfeld M., Watkins A.P., Yule A.J., Schønfeldt H., Simulation of agglomeration in spray drying installations: the EDECAD project, Drying Technol. 22 (2004) 1403–1462. [CrossRef] [Google Scholar]
- Verdurmen R.E.M., Straatsma H., Verschueren M., van Haren J.J., Smit E., Bargeman G., De Jong P., Modeling spray drying processes for dairy products, Lait 82 (2002) 453–463. [CrossRef] [EDP Sciences] [Google Scholar]
- Verdurmen R.E.M., Verschueren M., Gunsing M., Straatsma H., Simulation of agglomeration in spray dryers: the EDECAD project, Lait 85 (2005) 343–351. [CrossRef] [EDP Sciences] [Google Scholar]
- Westergaard V., Milk powder technology: evaporation and spray drying, Niro A/S, Søborg, Denmark, 1994, pp. 18–121. [Google Scholar]
- Williams A.M., Jones J.R., Paterson A.H.J., Pearce D.L., Effect of fines on agglomeration in spray dryers: an experimental study, Int. J. Food Eng. (2009) DOI: 10.2202/1556-3758.1635. [Google Scholar]
- Woo M.W., The simulation of spray drying under unsteady flow using CFD, 2008, private communications. [Google Scholar]
- Woo M.W., Daud W.R.W., Tasirin S.M., Talib M.Z.M., Controlling food powder deposition in spray dryers: wall surface energy manipulation as an alternative, J. Food Eng. 94 (2008) 192–198. [CrossRef] [Google Scholar]
- Woo M.W., Daud W.R.W., Tasirin S.M., Talib M.Z.M., Effect of wall surface properties at different drying kinetics on the deposition problem in spray drying, Drying Technol. 26 (2008) 15–26. [CrossRef] [Google Scholar]
- Wu Z.H., Liu X.D., Simulation of spray drying of a solution atomized in a pulsating flow, Drying Technol. 20 (2002) 1101–1121. [CrossRef] [Google Scholar]
- Xiao Z.F., Xie X.Y., Yuan Y.J., Liu X.D., Influence of atomizing parameters on droplet properties in a pulse combustion spray dryer, Drying Technol. 26 (2008) 427–432. [CrossRef] [Google Scholar]
- Xu P., Ray M.B., Mujumdar A.S., Yu B., Design and optimize hydrocyclones with CFD model, in: Proceedings of 8th World Congress of Chemical Engineering, 23–27 August 2009, Montreal, Canada (to appear). [Google Scholar]
All Figures
 |
Figure 1. Velocity magnitude contours for one-stage and two-stage HSDs: (a) one-stage HSD and (b) two-stage HSD (the fluidized bed covers the entire bottom boundary of this device simulated). |
| In the text | |
 |
Figure 2. Path-lines from the air inlet of drying chamber. |
| In the text | |
 |
Figure 3. Temperature contours at cut-planes X-Z and Y-Z. |
| In the text | |
 |
Figure 4. Axial velocity contours at different time intervals for (a) Case A and (b) Case A with smaller radius and higher flow rate (plan view is taken at 0.9 m from the ceiling). |
| In the text | |


